A text classification method by integrating mobile inverted residual bottleneck convolution networks and capsule networks with adaptive feature channels

Abstract

This study proposes a novel text classification model, MBConv-CapsNet, to address large-scale text data classification issues in the Internet era. Integrating the advantages of Mobile Inverted Bottleneck Convolutional Networks and Capsule Networks, this model comprehensively considers text sequence information, word embeddings, and contextual dependencies to capture both local and global information about the text effectively. It transforms from the original text matrix to a more compact and representative feature representation. A Capsule Network is designed to adaptively adjust the importance of different feature channels, including N-gram convolutional layers, selective kernel network layers, primary capsule layers, convolutional capsule layers, and fully connected capsule layers, aiming to enhance the model’s ability to capture semantic information of text across different feature channels. The use of the sparsemax function instead of the softmax function for dynamic routing within the Capsule Network directs the network’s focus more on capsules contributing significantly to the final output, reducing the impact of noise and redundant information, and further improving the classification performance. Experimental validation on multiple publicly available text classification datasets demonstrates significant performance improvements of the proposed method in binary classification, multi-classification, and multi-label text classification tasks, exhibiting better generalization capability and robustness.

Introduction

The rapid development of the Internet has generated a vast amount of textual data, including web pages, news articles, papers, e-books, chat content, emails, and user comments. The challenge of categorizing and organizing such massive amounts of textual data for rapid and accurate information retrieval is a fundamental research problem. In text classification tasks, three main types are commonly encountered: binary classification, multi-classification, and multi-label classification. Binary classification aims at categorizing texts into two mutually exclusive categories, such as positive and negative sentiments or positive and opposing viewpoints. Multi-classification tasks classify texts into multiple mutually exclusive categories, each belonging to only one category, such as news topic or question classification. Multi-label classification tasks allow a text to belong to multiple categories simultaneously, such as a news document involving multiple topics or aspects of sentiment. Each type of text classification task presents unique challenges and application scenarios. Understanding these distinctions is essential for developing accurate and effective text classification models.

Many traditional text classification models in the past were generally based on convolutional neural networks (CNN)¹ and recurrent neural networks (RNN)². The CNN-based text classification model extracts local features through convolutional layers and uses multiple convolution kernels to slide across different parts of the input text to capture local contextual information. The RNN-based text classification model structure recursively calculates information along the sequence direction through cyclic connections. It propagates features in a chain-like manner, which can capture the temporal features of sequence data. The text classification model based on LSTM³ introduces input gates, forget gates, and output gates to control the flow of information and effectively capture long-range dependencies. While CNN and RNN models effectively capture semantic and syntactic information, their pooling operations lead to semantic loss, limiting their text classification effectiveness. In recent years, Capsule Networks⁴ has been an emerging deep learning model. The core idea is to use capsules instead of neurons in convolutional neural networks, allowing the network to retain detailed pose information and spatial hierarchical relationships between objects, potentially addressing the information loss and classification limitations in traditional text classification methods. However, applying capsule networks to text classification still presents several challenges. First, capsule networks struggle to fully capture long-distance and positional dependencies in text, which are crucial for text classification. Second, they do not adequately address the importance of feature channels, failing to focus on critical textual information. Additionally, the dynamic routing algorithm⁵ between high-level and low-level capsules often generates noisy capsules, reducing training efficiency. In response to the limitations of existing text classification models, this paper proposes a novel text classification model: MBConv-CapsNet. This model integrates Mobile Inverted Residual Convolution (MBConv)⁶ and capsule network, optimizes capsule network structure, and improves the dynamic routing algorithm, aiming to solve the problems faced by existing CapsNet in text classification. The main contributions of this paper include:

• 1. A text classification method, which integrates Mobile Inverted Bottleneck Convolutional Networks and Capsule Networks, is proposed. It can fully consider the text’s sequence information, word embeddings, and contextual dependencies, effectively capturing local and global information and transforming the original text matrix into a more compact and representative feature representation.

• 2. This article designs a Capsule Network that adaptively adjusts the importance of different feature channels, including N-gram convolutional layers, selective kernel network layers, primary capsule layers, convolutional capsule layers, and fully connected capsule layers. This enhances the model’s ability to capture semantic information across various feature channels.

• 3. This article implements dynamic routing in the Capsule Network using the sparsemax function instead of softmax, ensuring that the network focuses on capsules that significantly contribute to the final output while ignoring less relevant ones. This reduces the model’s susceptibility to noise, enhancing its robustness and classification performance.

• 4. Experimental validation on multiple publicly available text classification datasets demonstrates significant performance improvements of the proposed method compared to previous text classification models in binary classification, multi-classification, and multi-label text classification tasks. This indicates superior generalization capability and robustness of the proposed approach.

Related work

From information retrieval to text data mining and natural language processing, text classification has always been a research hotspot, attracting considerable attention from academia and industry. Text classification techniques and methods have thus developed rapidly. Existing text classification methods mainly include traditional machine learning-based methods and deep learning-based methods.

Traditional machine learning-based text classification methods first use text representation methods such as the bag-of-words model⁷, TF-IDF features⁸, N-grams⁹, etc., to obtain feature vectors, and then select machine learning algorithms such as logistic regression¹⁰, naive Bayes¹¹, support vector machin¹², K-nearest neighbo¹³, and decision tree¹⁴ for classification. These traditional methods are time-consuming, requiring significant human intervention and extensive feature engineering.

With the development of deep neural networks, deep learning-based text classification methods have gradually become the mainstream of research. In 2014, Kim¹ proposed a CNN model suitable for text classification. Its main idea is to treat short texts of different lengths as matrix inputs, use multiple filters of various sizes to extract critical information from sentences, and use them for final classification. In 2015, Zhou³ et al. proposed Convolutional LSTM (C-LSTM), which first uses CNN to extract phrase-level semantic features and then feeds them into LSTM to determine the contextual dependencies between words. However, it must be trained in various ways, and using the entire text as input will lead to long training times. In 2017, Sabour⁵ et al. proposed updating the dynamic routing mechanism between primary and digital capsules to obtain higher-level entity representations. In 2018, Zhao¹⁵ et al. constructed a text classification model based on capsule networks (Capsule-A, Capsule-B), using parallel convolutional filtering windows to learn more comprehensive text information, and the text classification effect is better than CNN and LSTM. In 2022, Jia¹⁶ et al. proposed a capsule network model that combines multi-head attention and graph convolutional neural networks in parallel to integrate syntactic information. In 2022, Wang¹⁷ et al. proposed a text classification method based on LSTM and graph attention networks. In 2024, Guo¹⁸ et al. proposed a model integrating BERT encoders with capsule networks, using capsule layers instead of traditional fully connected layers for downstream classification tasks in BERT. Although the above capsule network models obtain multi-scale and multi-grammar text features through average pooling, the way of feature fusion is unreasonable because it ignores that the various scale grammar features corresponding to individual words in the text should not be equally essential but should be determined by specific contexts. In addition, Wang¹⁹ et al. found that in the routing algorithm of capsule networks, sub-capsules will be routed to each parent capsule, which will cause some capsules to become noisy capsules. Although deep learning offers new opportunities for text classification, existing research on capsule networks still needs to improve the handling of textual data. Inspired by the above ideas, this paper proposes a text classification method that combines mobile inverted residual bottleneck convolution and capsule networks to obtain advanced local information, aiming to overcome existing models’ limitations and improve text classification performance and efficiency.

Model design

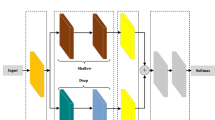
The existing Capsule Network needs help to fully capture contextual information and semantic relationships in text classification tasks. It also needs to adapt more effectively to the dynamic complexity of text data, with routing weight distributions that are too smooth to emphasize the contributions of critical capsules. This paper introduces the MBConv-CapsNet model to address these limitations. By integrating MBConv modules with capsule networks, the model optimizes the Capsule Network structure and enhances the dynamic routing algorithm, improving performance in text classification. The model framework is shown in Figure 1.

Figure 1

Network architecture diagram of MBConv-CapsNet.

The model uses a sentence matrix as input:

$$\begin{aligned} X = [{x_1},{x_2}, \ldots ,{{\textrm{x}}_{n - 1,}}{x_n}] \in {R^{L \times d}} \end{aligned}$$

(1)

Where ${x_i} \in {R^C}$ represents the word vector of the $i^{th}$ word in the sentence, n is the number of words, L is the length of the input text, d is the dimension of the input features, and $L \times d$ is the dimension of the word vector. Here, B denotes the number of N-gram convolutional layers, C is the number of transformation matrices in the central capsule layer, D is the number in the convolutional capsule layer, and E represents the number of capsules in the fully connected layer.

Mobile inverted residual convolution module

Text data in classification tasks often present in high-dimensional, sparse forms, making feature extraction challenging. Traditional text classification models typically need help to capture contextual information and semantic relationships in complex text, with high dimensionality and sparsity compounding these challenges. This paper employs the MBConv module as the model’s initial layer to address these issues, allowing for efficient feature extraction from input text data. MBConv effectively captures local and global features in text and generates compact, expressive feature representations through its depthwise separable convolution and inverted residual structure. This preprocessing enhances the capsule network’s text-processing capabilities and enables it to capture contextual information and semantic relationships in the text.

This work uses an optimized version of MBConv from Google’s EfficientNet²⁰, a lightweight network proposed in 2019. Following the “lightweight and efficient” design principle, it builds a structure capable of extracting input features efficiently. Specifically, MBConv consists of four components: a standard convolutional layer, a depthwise separable convolutional layer, an SE network layer²¹, and a pointwise convolutional layer. The depthwise separable convolution k is set to 3 in this implementation, as shown in Fig. 2.

Figure 2

Diagram of mobile inverted residual convolution module.

Standard Convolutional Layer: This module combines 1$\times$1 convolutional kernels, a Batch Normalization (BN)²² layer, and the Swish²³ activation function. This design allows low-dimensional sentence matrices to increase feature dimensionality while preserving resolution. The time complexity of this layer is $O(L \times d)$.

Depthwise Separable Convolutional Layer: This layer integrates 3$\times$3 depthwise separable convolutional kernels²⁴, a BN layer, and the Swish activation function. The core concept is to use a 3x3 convolution kernel to implement channel-by-channel deep convolution for each group, that is, to perform a single filter convolution on each channel, aiming to collect local features of each channel. The time complexity of this layer is $O(L \times d \times k)$.

SE Network Layer: The SENet attention mechanism is applied along the channel dimension by assigning specific weights to each channel and multiplying them with the feature map, allowing the model to emphasize informative channel features and reduce the influence of less relevant ones. This process involves three operations: first, the Squeeze operation compresses the input feature map into a vector through a global average pooling operation. Next is the Excitation operation, a mechanism similar to gates in recurrent neural networks. By increasing the dimension of feature mapping, the network can more effectively capture global features at higher dimensions, especially when dealing with correlations between multiple channels. Finally, the Scale operation uses the weights from the Excitation step to recalibrate the original feature map through channel-wise multiplication, refining the feature representation along the channel dimension. The time complexity of this layer is $O(L \times d)$.

Pointwise Convolutional Layer: This module consists of 1$\times$1 convolutional kernels, BN, and Dropout layers. The 1$\times$1 kernels reduce dimensionality, the BN layer normalizes batches, and Dropout randomly drops parameters to prevent overfitting and speed up convergence. The time complexity of this layer is $O(L \times d)$.

The final time complexity of the MBConv module can be simplified as $O(L \times d + L \times d \times k)$. The design of MBConv optimizes convolution operations by decomposing standard convolutions into depthwise separable convolutions, significantly reducing computational complexity. It is suitable for extracting high-dimensional text features and accelerating training and inference on large-scale datasets. This article uses the MBConv module as the initial layer of the model to extract features from the input text data. This preprocessing method not only improves the ability of subsequent capsule networks to process text data but also helps the model better capture contextual information and semantic relationships in the text.

Capsule network module

The Capsule Network module in the proposed MBConv-CapsNet model consists of five components: the N-gram convolutional layer, Selective Kernel Network (SKNet)²⁵ layer, primary capsule layer, convolutional capsule layer, and fully connected capsule layer. The SKNet layer is introduced before the primary capsule layer to enhance feature extraction, allowing the model to dynamically adjust the importance of various feature channels and more effectively capture critical textual information. Additionally, the sparsemax function²⁶ replaces the softmax function²⁷ in the dynamic routing algorithm, promoting a sparser distribution of routing weights and improving the model’s ability to identify essential information. The capsule network architecture is illustrated in Fig. 3.

Figure 3

Network architecture diagram of CapsNet.

The first layer is the N-gram convolutional layer. For ${x_i} \in {R^{L \times d}}$, let ${W^a} \in {R^{{P_1} \times d}}$ be the filter for the convolutional operation, where $P_1$ is the N-gram size when sliding on the sentence to detect features at different positions. The filter ${W^a}$ convolves with the word window ${{\textrm{X}}_{i:i}} + {P_1} - 1$ at every possible position to generate a column feature map $m_i^a \in {R^{L - {P_1} + 1}}$, and each element $m_i^a \in R$ of the feature map is generated by

$$\begin{aligned} m_i^a = \delta (({{\textrm{X}}_{i:i}} + {P_1} - 1) \circ {W^a} + {{\textrm{b}}_0}) \end{aligned}$$

(2)

Among them, $\circ$ is element-wise multiplication, $b_0$ is the bias term, and $\delta$ is the nonlinear activation function ReLU²⁸. Therefore, for $a = 1,...,B$, a total of B filters with the same N-gram size can generate B feature maps. The time complexity of this layer is $O(L \times d \times B)$, and these feature maps can be rearranged into a feature matrix:

$$\begin{aligned} {\textrm{M}} = [{m_1},{m_2}, \ldots ,{m_B}] \in {R^{(L - {P_1} + 1) \times B}} \end{aligned}$$

(3)

The capsule network model proposed in this article adds a selective kernel network layer between the N-gram convolutional layer and the main capsule layer, responsible for feature screening and enhancement. It adapts to different input data by dynamically selecting convolution kernels, thereby achieving adaptive feature extraction. This layer uses two convolution kernels with kernel sizes of $K_1$ and $K_2$ for convolution. The time complexity of this layer is $O(L \times d \times ({K_1} + {K_2}))$. The feature map is generated through three steps segmentation, fusion, and selection:

$$\begin{aligned} {\textrm{V}} = [{v_1},{v_2}, \ldots ,{v_B}] \in {R^{(L - {P_1} + 1) \times B}} \end{aligned}$$

(4)

The third layer is the main capsule layer, which converts the features output by the N-gram convolutional layer into capsule representations. Let ${o_i} \in {R^d}$ represent the instantiation parameters of the capsule, and ${W^b} \in {R^{B \times d}}$ represent the filters shared by different sliding windows. For each matrix multiplication, we have a window sliding over each N-gram vector, represented as ${{\textrm{V}} _i} \in {R^B}$, and then generate the corresponding N-gram phrase ${o_i} = {({W^b})^T}{{\textrm{V}} _i}$ in capsule form. The filter ${W^b}$ multiplies each N-gram vector in $\left\{ {{{\textrm{V}} _i}} \right\} _{i = 1}^{L - {P_1} + 1}$ with a stride of 1 to create a capsule column list $o \in {R^{\left( {L - {P_1} + 1} \right) \times d}}$, where each capsule oi in the column list is calculated as

$$\begin{aligned} {o_i}{\mathrm{= }}g\left( {{W^b}{{\textrm{V}} _i} + {{\textrm{b}} _1}} \right) \end{aligned}$$

(5)

Where g is the nonlinear squeezing function of the entire vector, and $b_1$ is the capsule bias term. For all C filters, the generated capsule feature maps can be rearranged as follows:

$$\begin{aligned} {\textrm{O}} = [{o_1},{o_2}, \ldots ,{o_C}] \in {R^{(L - {P_1} + 1) \times C \times d}} \end{aligned}$$

(6)

Among them, $(L - {P_1} + 1) \times C \times d$ is the dimension of the primary capsule matrix P, and this layer’s time complexity is $O(L \times C \times {d^2})$.

The fourth layer is the convolutional capsule layer, where each capsule is only connected to a local region ${P_2} \times C$ in the lower layer space. These capsules in this region are multiplied by a transformation matrix to learn the parent-child relationship and then routed according to the protocol to generate parent capsules in the upper layer. Let ${W^{\textrm{c}}} \in {R^{D \times d \times d}}$ represent the shared weight, where ${P_2} \times C$ is the number of sub-capsules in the lower local area, and D is the number of parent capsules sent by the sub-capsules. The weights of high-level capsules and low-level capsules are obtained through dynamic routing as follows:

$$\begin{aligned} {\hat{u}_{j|i}}&= W_j^c{u_i} + {\hat{b}_{j|i}} \end{aligned}$$

(7)

$$\begin{aligned} {{\textrm{s}}_j}&= \sum \limits _i {{{\textrm{c}}_{ij}} \cdot {{\hat{u}}_{j|i}}} \end{aligned}$$

(8)

Among them, ${\hat{b}_{j|i}}$ is the capsule bias term, ${u_i}$ is the sub-capsule in the local area ${P_2} \times C$, $W_j^c$ is the $j^{th}$ matrix in the tensor ${W^c}$, and ${{\textrm{c}}_{ij}}$ is the coupling coefficient updated through a dynamic routing algorithm. The time complexity of this layer is $O(L \times D \times {d^2})$. We use a dynamic routing protocol to generate a total of $(L - {P_1} - {P_2} + 2) \times D \times d$ dimensional feature maps of parent capsules in this layer:

$$\begin{aligned} {\textrm{U}} = [{u_1},{u_2}, \ldots ,{u_{\textrm{D}}}] \in {R^{(L - {P_1} - {P_2} + 2) \times D \times d}} \end{aligned}$$

(9)

The fifth layer is the fully connected capsule layer, responsible for converting the output of the convolutional capsule layer into the final capsule vector representation, mapping the capsule vectors to the classification label space through fully connected operations, and generating the final capsule ${y_j} \in {R^d}$. Each capsule in this layer represents a possible category, and by calculating the activation level of each capsule, the probability of the input text belonging to which category can be determined, which is used to form capsules representing categories:

$$\begin{aligned} {\textrm{Y}} = [{y_1},{y_2}, \ldots ,{y_E}] \in {R^{E \times d}} \end{aligned}$$

(10)

Here, E is the number of categories plus the number of additional isolated categories. This layer’s time complexity is $O(E \times {d^2})$. Figure 4 shows the capsule’s working principle.

Figure 4

Schematic diagram of capsule working principle.

The final time complexity of the capsule network module can be simplified as $O(L \times (d \times B + d \times ({K_1} + {K_2}) + C \times {d^2} + D \times {d^2}) + E \times {d^2})$. On text datasets, the computational complexity of MBConv and capsule network modules is proportional to the model’s size and the input data’s dimensionality. The main cost of the capsule network module in terms of time complexity comes from the dynamic routing mechanism, which may lead to computational bottlenecks due to the need for iterative updates of routing weights. By optimizing the time complexity of the above modules and combining them with efficient hardware support, the training efficiency and inference speed of the model on large-scale text datasets can be effectively improved.

Selective kernel network module

While capsule networks effectively process structured data such as images, they may need help fully capturing text classification tasks’ dynamic and complex nature. Critical information can be distributed across various words or phrases in text data, necessitating the model’s ability to adapt its focus. Incorporating the SKNet layer into the capsule network enables the model to dynamically adjust the importance of different feature channels. The SKNet layer computes the weights for each feature channel based on the input text’s representation, generating a refined feature representation through weighted summation. This adaptive mechanism allows the model to prioritize feature channels relevant to specific text data, thereby enhancing classification performance.

SKNet, proposed by Xiangyu Li et al. at CVPR 2019, is an attention mechanism designed to improve the model’s representative capacity by dynamically selecting features of different scales. By introducing SKNet before the primary capsule layer, the model can better capture critical text information by weighting and merging feature maps of varying scales, enhancing classification accuracy. The SKNet module has three main stages: Split, Fuse, and Select, as illustrated in Fig. 5.

Figure 5

Schematic diagram of SKNet module.

In the Split stage, the input text feature map $X \in {R^{H \times W \times C}}$ is divided using convolutional kernels of different sizes, $K_1$ and $K_2$, producing two feature maps, $\tilde{F}:X \rightarrow {F_1} \in {R^{H \times W \times C}}$ and $\hat{F}:X \rightarrow {F_2} \in {R^{H \times W \times C}}$. The time complexity of this operation is $O(L \times d \times ({K_1} + {K_2}))$.

In the Fuse stage, neurons adjust their receptive field size adaptively in response to the content of the input stimulus. The key concept is to use gates to control the flow of multi-scale information across branches to the next layer, where these branches contain information of different spatial scales. First, the outputs of the two branches are combined by element-wise summation:

$$\begin{aligned} {\textrm{F}} = {F_1} + {F_2} \end{aligned}$$

(11)

Global average pooling is then used to embed global context, generating channel-wise statistical information ${\textrm{s}} \in {R^C}$. Specifically, the ${c^{th}}$ element of s is computed by contracting F across spatial dimensions H$\times$W:

$$\begin{aligned} {{\textrm{s}}_c} = {\mathcal{F}_{gp}}({F_c}) = \frac{1}{{H \times W}}\sum \limits _{i = 1}^H {\sum \limits _{j = 1}^W {{F_c}(i,j)} } \end{aligned}$$

(12)

Additionally, a compact functional component ${\textrm{z}} \in {R^{d \times 1}}$ provides precise and adaptive selection guidance through a fully connected layer, which reduces dimensions to improve efficiency:

$$\begin{aligned} {\textrm{z}} = {\mathcal{F}_{fc}}(s) = \delta (\beta (Ws)) \end{aligned}$$

(13)

Here, $\delta$ represents the ReLU activation function, $\beta$ denotes batch normalization, and ${\textrm{W}} \in {R^{d \times C}}$, r control the dimension d to optimize model efficiency:

$$\begin{aligned} d = \max (C/r,L) \end{aligned}$$

(14)

L, set to 32 in this experiment, represents the minimum dimension. The time complexity of this operation is $O(L \times d)$.

In the Select stage, soft attention across channels is applied to adaptively select information at different spatial scales, guided by compact feature descriptors z. Specifically, the softmax function is used across channels. The final feature map Y is generated by applying attention weights across multiple kernels, integrating multi-scale information from various receptive fields. The time complexity of this operation is $O(L \times d + L)$.

The final time complexity of the SKNet module can be simplified as $O(L \times d \times ({K_1} + {K_2}))$. Its complexity mainly focuses on the dimension transformation of multi-scale convolution and fully connected layers. Although the module increases the computational cost of the model, it also enhances its ability to select multi-scale features. Optimizing the convolution kernel size and scaling factor is necessary to balance complexity.

Dynamic routing module

Dynamic routing in capsule networks involves iteratively constructing a nonlinear mapping to transmit information from lower to higher-level capsules and determine their activation states. The original dynamic routing algorithm uses the softmax function to ensure non-negativity and normalization of routing weights, enabling the model to learn the relative importance of capsules. Its formula is defined as:

$$\begin{aligned} {{\textrm{softmax}} _i}(z) = \frac{{\exp ({z_i})}}{{\sum \nolimits _j {\exp ({z_j})} }} \end{aligned}$$

(15)

Where $z$ represents the input vector. From the formula, it can be observed that after softmax computation, the element weights are all non-zero. This implies that even elements irrelevant to the query are allocated a small weight, leading to all elements having some degree of influence on the prediction. This might result in assigning high weights to unimportant information and failing to effectively highlight key capsules’ contributions. This paper proposes using the sparsemax function instead of softmax to improve the dynamic routing algorithm. The sparsemax function can generate sparse weight vectors, concentrating routing weights more on a few critical capsules, thereby better highlighting their contribution to the classification task. Its formula is defined as:

$$\begin{aligned} {\textrm{sparsemax}} (z) = \mathop {\arg \min }\limits _{p \in {\Delta ^{K - 1}}} ||p - z|{|^2} \end{aligned}$$

(16)

Where $p \in {\Delta ^{K - 1}}$, ${\Delta ^{K - 1}}$ is a (K-1)-dimensional simplex.The sparsemax function in this paper returns the Euclidean projection of the input vector $z$ onto the K-1 dimensional probability simplex, where these projections are likely to touch the boundary of the simplex, resulting in some probability values becoming zero, thus obtaining a sparse probability distribution.

The original dynamic routing algorithm uses the softmax function to calculate the coupling coefficient, iteratively updates it, and has a time complexity of $O(D \times L \times {d^2} \times T)$. Among them, T is the number of dynamic routing iterations. Sparse dynamic routing has slightly lower time complexity as it only calculates non-zero probability distributions. The time complexity is $O(D \times L \times {d^2} \times {T_{sparse}})$, where ${T_{sparse}}$ is the number of sparse dynamic routing iterations. Dynamic routing is the main source of time complexity in capsule networks. The sparse dynamic routing module generates sparse weight vectors, reducing the number of calculations and effectively reducing time complexity. It is particularly suitable for large-scale text datasets and can improve computational efficiency while maintaining accuracy. The comparison between the softmax and sparsemax functions is shown in Fig. 6.

Figure 6

Comparison diagram of softmax function and sparsemax function in 2D (left) and 3D (right two).

From the figure, it can be observed that sparsemax is piecewise linear, but the asymptotic curve is similar to softmax. This sparsity helps the capsule network pay more attention to capsules that contribute more to the final output during routing and ignore those with smaller contributions. Moreover, using the sparsemax function can also improve the computational efficiency of the model, reducing redundant computations. This helps reduce the model’s reliance on noise information, improve its robustness, enhance the performance of capsule networks in tasks such as text classification, and promote the development of capsule networks in deep learning.

Experimental results and analysis

This study evaluates the proposed MBConv-CapsNet model through experiments on four well-known public text classification datasets, including binary, multi-class, and multi-label classification tasks. The model’s effectiveness is validated through performance improvements across multiple evaluation metrics.

Experimental setup

In the experiment, the experimental model input uses a 300-dimensional Word2Vec²⁹ pre-trained word vector, and the training process uses an Adam³⁰ optimizer to minimize the objective function. The capsule dimension is set to 16. During the experiment, the larger the size of the text data, the higher the memory usage, the longer the training time, and the greater the computational resources. The gradual increase in the learning rate will accelerate the convergence speed of the learning algorithm, leading to an unstable learning process. As the batch size increases, the memory usage becomes more extensive, but the training accuracy still needs to improve significantly. The training rounds on the validation set generally converge between 30 and 50 rounds. Therefore, the learning rate of this experiment is set to 1e−3, the batch size is 25, the training batch epoch is 50, and the number of iterations of the dynamic routing algorithm is 3 to optimize the loss faster and ultimately converge to a lower loss. In our experiment, all models were run on servers using the Ubuntu 16.04 operating system, GeForce RTX3090 GPU, 200 GB of memory, Inter Xeon E5 V3 2600 CPU, and Pytorch 1.10 deep learning framework.

Experimental datasets

The datasets used in this study comprise movie reviews (MR)³¹, the Subjectivity dataset (Subj)³², the TREC question dataset (TREC)³³, and Reuters-21578³⁴. MR and Subj are utilized for single-label binary classification tasks. TREC and Re-Single are utilized for single-label multi-classification tasks, while Re-Full and Re-Multi are employed for multi-label text classification tasks. The specific descriptions of the experimental data are presented in Table 1.

Evaluation metrics

To more accurately evaluate the classification results, this study employs the following evaluation metrics: accuracy (Acc), exact match rate (ER), micro-precision (Pre), micro-recall (Recall), micro-F1 score (F1), and margin loss (ML). Acc is used as the evaluation metric in single-label text classification experiments, while ER is used as the metric in multi-label text classification experiments.

Table 1 Description of experimental datasets.

Comparative experiments

To further verify the performance of the MBConv-CapsNet model, we conducted comparative experiments with text classification models based on KimCNN, C-LSTM, Capsule-A, Syntax AT Capsule, and LSTM-GAT as baseline models. KimCNN is a classic text classification model based on CNN; C-LSTM first uses CNN to extract phrase-level semantic features, which are then sent to LSTM to determine the contextual dependencies between words; Capsule-A is a text classification model based on capsule networks; Syntax AT Capsule is a capsule network model that combines multi-head attention and graph convolutional neural networks in parallel to fuse syntactic information; LSTM-GAT is a text classification method based on LSTM and graph attention network. In Acc, Pre, Recall, and F1, a “+” indicates that a higher value corresponds to better model performance. In the ML column, a “-” indicates that a smaller value indicates better model performance, with the best experimental results shown in bold font. For the convenience of comparison, our model and other baselines used Margin loss during the experimental process. Performance comparison was conducted under the same configuration environment and initial training parameters. Experimental results indicate that the proposed MBConv-CapsNet model significantly improves across five critical metrics for binary, multi-class, and multi-label text classification tasks. The experimental results are shown in Tables 2, 3, and 4.

Table 2 Performance comparison of text classification on binary classification datasets.

Table 3 Performance comparison of text classification on multi-class classification datasets.

Table 4 Performance comparison of text classification on multi-label classification datasets.

It can be observed that the model presented in this article outperforms other baseline models, and capsule-based methods typically outperform general neural network methods such as KimCNN and C-LSTM. KimCNN performs similarly to C-LSTM, with KimCNN focusing more on local information in the text, while C-LSTM can capture contextual semantic information in the text. The model presented in this article is superior to general neural network methods, indicating that capsule networks use capsules instead of neurons in neural networks. The model can preserve detailed pose information and spatial hierarchical relationships between objects to a greater extent. Syntax AT Capsule performs well in experiments on various datasets by using GCN to extract syntactic structure information from syntactic dependency trees. Still, it requires a large amount of memory and longer training time. Due to large-scale pre-training, Syntax AT Capsule has an acc value 0.1% higher than our model on the ReFull dataset and a recall value 0.3% higher than our model on the Re Multi dataset. In terms of overall performance, the model proposed in this paper is significantly better than Syntax AT Capsule, as MBConv can extract more features with less computational complexity, which performs well in modeling complex text structures. LSTM-GAT performs well in single-label text classification, but there is a significant performance gap compared to our model in multi-label text classification. This is because the dynamic routing mechanism in the capsule network can help the model better learn the potential associations between labels, thereby accurately capturing multi-label relationships in multi-label tasks, especially when there are similar or dependent relationships between labels. This article also draws a line chart to observe the classification performance of each model, as shown in Figure 7. A red line represents our model in the figure.

Figure 7

Model performance comparison across different datasets.

Ablation experiments

This article conducted ablation experiments to verify the effectiveness of each module in the MBConv-CapsNet model, including the Mobile Inverted Bottleneck Convolution module, improved capsule network, and optimized dynamic routing algorithm. The impact of each module on binary, multiclass, and multilabel text classification tasks was evaluated under consistent experimental conditions. Capsule-A is the original text classification model based on capsule networks. M1, M2, and M3 add a mobile bottleneck re-versal convolution module, a selective kernel network module, and a dynamic routing module to the Capsule-A model. M4 adds a mobile bottleneck flipping convolution module and a selective kernel network module to the Capsule-A model. Ours adds a mobile bottleneck flipping convolution module, a selective kernel network module, and a dynamic routing module to the Capsule-A model. The experimental results are shown in Tables 5, 6, and 7.

In M1, the MBConv module was added to the experiment. There is no significant performance improvement on binary classification datasets because the MBConv module belongs to a lightweight convolutional network design and performs well in extracting complex text structure information. Therefore, the importance of the MBConv module in our model is more evident in MR.

Table 5 Ablation experiments on binary classification datasets.

Table 6 Ablation experiments on multi-class classification datasets.

Table 7 Ablation experiments on multi-label classification datasets.

The SKNet module was added to the experiment in M2. The SKNet module performs better on multi-class datasets, indicating that it can adaptively adjust the importance of feature channels and better capture critical information in text.

In M3, our Routing was added to the experiment. It can be seen that there is no significant performance improvement on the multi-label text classification dataset because the sparsity of the sparsemax function helps the capsule network to focus more on those capsules that contribute more to the final output during the routing process while ignoring those that contribute less. At this point, with the support of MBConv and SKNet modules, the model would retain some text information, resulting in a decrease in text classification performance.

In M4, both MBConv and SKNet modules were added to the experiment. The model’s classification performance has been significantly improved on various datasets. The MBConv layer can capture text features of different granularities through multi-scale convolution. The SKNet module allows the network to adaptively select the appropriate convolution kernel size based on input data, capturing features at different scales. This design enhances the model’s ability to handle multi-scale information and effectively reduces the risk of overfitting.

The experimental results show that adding our Routing to M4 enables the model to focus on the most informative Routing while ensuring accuracy and higher computational efficiency. In summary, this model is robust and universal when dealing with various text data types.

Routing iterations experiments

Capsule networks generate textual capsules through iterative updates using the dynamic routing algorithm. To evaluate the influence of routing iteration count on experimental results, experiments are conducted on the Re-Full dataset, and learning curves are plotted to demonstrate the nature of different routing iterations, as shown in Table 8.

Table 8 Performance comparison of different routing iteration counts.

When the routing count is low, the capsule network fails to learn input representations of sequential models sufficiently. As the iteration count increases, the algorithm tends to converge when the routing count reaches 3; however, further increases in iteration count lead to overfitting during the training process, resulting in decreased classification performance. Therefore, a routing iteration count of 3 is selected.

Discussion and conclusion

This study’s proposed MBConv-CapsNet model presents a practical approach for classifying large-scale textual data, addressing the complexities of modern text classification tasks. By integrating the Mobile Bottleneck Convolutional Network and Capsule Network, the model comprehensively captures various aspects of textual information, effectively enhancing the accuracy and efficiency of text classification. Adopting the Capsule Network structure with adaptive adjustment of feature channel importance and using the sparsemax function for dynamic routing further strengthen the model’s ability to capture critical information and resist noise. Experimental results demonstrate significant advantages of MBConv-CapsNet across various text classification tasks, indicating its broad application prospects. However, the current model relies heavily on training data, and in medical literature and legal documents with special text data distributions, a large amount of professional data may be required for pre-training and fine-tuning. In addition, in practical applications, models often need to make predictions on categories of unseen test samples, which involves zero-shot learning. It can mine the mapping relationship between the features and labels of seen class samples and then transfer it to predictions of unseen classes. Therefore, our future research will focus on utilizing existing feature extraction mechanisms and capsule network structures combined with shared feature strategies in cross-modal learning to provide reasonable semantic representations for unseen categories, thereby improving performance in zero-shot learning scenarios.