A spatio-temporal graph wavelet neural network (ST-GWNN) for association mining in timely social media data

Abstract

Social media generates vast amounts of spatio-temporal sequential data. However, current methods often ignore the complex spatio-temporal correlations within these data. This oversight makes it difficult to fully capture the dynamic features of the data. To delve deeply into the concealed feature attributes within timely spatio-temporal sequence data from social media, this study introduces a Spatio-Temporal Graph Wavelet Neural Network (ST-GWNN). This model captures spatio-temporal correlations across time and space by combining spatial graphs from multiple time intervals. On this basis, we have developed a spatial feature extraction layer using the Graph Wavelet Neural Network (GWNN). This layer learns localized representations of node features to identify spatial dependencies. In GWNN, graph wavelet transformation reduces computational complexity and improves operational efficiency compared to Spectral CNN. Furthermore, the sparse representation of node features is enhanced via localized learning, thereby improving network performance. The effectiveness of the model is verified using four distinct social media datasets. Experimental results underscore the notable advantages of the proposed model in the realm of timely time-series data association mining, showcasing its capacity to better capture spatio-temporal dynamics and uncover the underlying association mining within the data. In comparison to alternative models, the approach outlined in this paper exhibits substantial improvements in terms of accuracy and efficiency, affirming the efficacy and innovation of the model.

Introduction

The Internet’s rapid evolution favors Browser/Server (B/S) architecture over Client/Server (C/S). This shift coincides with the rise of web applications during the Web 2.0 era. Among these web applications, social media has emerged and attracted a large number of users, becoming a highly active and heavily trafficked platform on the internet^1,2,3. Facebook, Twitter, and Weibo, according to Alexa’s authoritative ranking, all occupy positions in the Top 20⁴. The Internet Network Information Center released the 52nd Statistical Report on Internet Development. The report shows that as of June 2023, the number of Internet users reached 1.079 billion, an increase of 11.09 million from December 2022, and the Internet penetration rate reached 76.4%. Social media platforms such as Weibo, WeChat, Xiaohongshu, TikTok, and Kwai, dominate the social media landscape, boasting substantial user engagement. The user base of these platforms continues to grow annually, reflecting the increase in overall Internet usage. With the participation of a large number of users, social media generates a wide range of user activity information, including text, audio, and video. Recognizing the potential to extract valuable insights, researchers are increasingly focusing on social media data analysis^5,6,7.

Spatio-temporal data, characterized by timestamped entries and geolocation tags, exemplifies this data type. This data captures user activities across various temporal points, forming time series that can be mined to discern patterns in user engagement, shifts in popular topics, and the diffusion of events. The geolocation capabilities inherent in many platforms facilitate the analysis of regional user behaviors and social dynamics. The spatio-temporal nature of this data allows for the exploration of correlations across time and space. The timeliness of the data highlights its significance, emphasizing the importance of collecting and recording it within a specific timeframe.

Social media data are spatio-temporally complex, involving multiple sources, variables, and scales. They are characterized by massive data volumes, correlations, and heterogeneity. As mobile Internet and artificial intelligence advance rapidly, they generate vast amounts of structured and unstructured data. The relationships between these data are becoming more intricate^8,9,10. In this context, detecting anomalies within social media data becomes crucial. Recent approaches, such as those utilizing Sparse Canonical Correlation Analysis combined with Random Masking and Padding, have shown effectiveness in identifying anomalies in attributed networks¹¹. Furthermore, techniques involving residual-enhanced graph convolutional networks with hypersphere mapping provide advanced methods for anomaly detection, highlighting the evolving landscape of detection strategies in complex networks¹².

Association mining in social media uncovers the underlying mechanisms and relationships between different elements. It shows how a user’s actions within a group can influence others, such as a military enthusiast becoming interested in history. This process helps identify correlations in user interactions, visualize information flow, and predict public opinion trends. Additionally, the use of dual variational autoencoders with generative adversarial networks enhances the detection of anomalous nodes in attributed social networks, further illustrating the importance of sophisticated techniques in this field¹³. Moreover, a pilot study on various anomaly detection methods emphasizes the necessity for robust frameworks to analyze the intricacies of online social networks¹⁴. These advancements underscore the critical need for effective methods to analyze the dynamic and interconnected nature of social media data. Lastly, an extensive review on dark web threats and detection techniques highlights how similar methods can be adapted for anomaly detection in broader contexts, reinforcing the relevance of these strategies in social media analysis¹⁵.

Spatio-temporal data mining, a leading frontier in data mining research, has garnered significant attention from the academic community^16,17,18,19. The spatio-temporal data of the target can reflect the movement patterns and laws of the object. The behavioral patterns of the target entity can be mined using these data, and its next behavior can be predicted based on these patterns. Therefore, it has a wide range of applications in the fields of traffic, rainfall, environmental monitoring, meteorological disasters, socio-economics, epidemiology, and social media^{20,21,22,23,24}.

In the context of social media application, Dai et al.‘s²⁵ work on sentiment analysis using LSTM models is significant as it addresses the temporal aspect of user sentiment, which is crucial for understanding the evolution of opinions and emotions over time. This approach can be particularly useful for tracking public sentiment during events like elections, product launches, or crises. Xiong et al.‘s²⁶ proposal to use spatio-temporal graphical convolutional networks for behavior analysis introduces a spatial dimension to the analysis, which is essential for understanding how geographic proximity influences social interactions and information spread. Their method of constructing user relationships into a graph and applying convolutional networks to this structure is a step forward in modeling the complex interconnectivity of social media networks. Ma & Gan’s²⁷ research on interest evolution through spatio-temporal clustering provides insights into how user interests can be modeled over time, taking into account the sequence of user activities. This approach can be highly beneficial for content recommendation systems that aim to adapt to the changing preferences of users. Xu et al.²⁸ contribute by presenting a method for data detection in social media using graph neural networks with hierarchical aggregated features. Their innovative approach leverages Graph Convolutional Networks (GCNs) with propagation graphs to capture nuanced text representations of event propagation dynamics. Their method enhances the detection of critical social media events by using Graph Neural Network (GNN) models, which update aggregated features at both word and text levels through document graphs. This improves upon existing techniques for data detection and analysis in dynamic online environments. Meanwhile, Mutinda et al.²⁹ focus on advancing sentiment analysis by enriching word embeddings with subjective knowledge. Their approach integrates deep semantic understanding into word embeddings, enhancing sentiment classification models’ accuracy. By incorporating subjective knowledge, they address limitations of traditional sentiment analysis techniques that often overlook subtle nuances in user sentiment expressed through social media. This innovation not only improves the precision of sentiment analysis but also expands the applicability of sentiment analysis models across diverse domains, from product reviews to social media discussions.

The current spatio-temporal models in the field of social media data mining primarily suffer from the following limitations:

(1) Insufficient capability for high-dimensional data processing: Traditional methods often struggle with the high dimensionality of social media data, hindering the comprehensive extraction of valuable patterns. These models may not effectively handle and interpret the complex relationships and patterns within the data.

(2) Limited ability to capture dynamic changes: Current models frequently fail to capture the dynamic evolution of social media content and user interactions over time (as highlighted in references. This means that these models may not accurately predict and analyze trends in information flow and public sentiment.

(3) Lack of integrated spatial and temporal correlation: There is a deficiency in models that can effectively integrate spatial and temporal correlations within a unified framework for analyzing social media data. This limits the model’s ability to capture spatio-temporal dynamics when analyzing social media data.

(4) Inadequate representation of localized features: Existing models may not adequately represent localized node features, which is a critical issue in graph neural networks. This affects the model’s ability to capture local spatial dependencies.

In response to these limitations, the proposed ST-GWNN model takes the following measures to overcome these challenges:

(1) Fusion of spatial graphs across multiple time intervals: ST-GWNN captures spatio-temporal correlations by fusing spatial graphs from multiple time intervals, which helps the model better understand the complex spatio-temporal dynamics in social media data.

(2) Graph Wavelet Neural Network (GWNN): This study developed GWNN spatial feature extraction layer learns localized representations of node features to identify spatial dependencies. The graph wavelet transformation reduces computational complexity and improves operational efficiency compared to Spectral CNN, enhancing performance.

(3) Enhanced sparse representation of local features: By enhancing the sparse representation of node features through localized learning, the model’s performance is improved, allowing it to more accurately capture local spatial dependencies in social media data.

(4) Unified framework for spatial and temporal dependencies: ST-GWNN provides a unified framework that can handle both spatial and temporal dependencies within social media data, leading to a more comprehensive analysis.

(5) Applicability to real-world scenarios: The model is designed with real-world application scenarios in mind, such as targeted advertising, content recommendation, crisis management, and social media platform optimization, offering insights that can be utilized in these contexts.

The innovative points of this study are as follows:

1) Directly fusing spatial maps of multiple time steps can efficiently extract features pertinent to association mining in the spatio-temporal dimension. This approach enhances the model’s ability to capture complex relationships within social media data.

2) By using multi-feature extraction techniques and graph wavelet convolution, our model performs better in predicting social media trends and user behaviour.

3) Integrating graph wavelet neural network techniques into spatio-temporal data mining for social media to improve prediction performance and mining efficiency.

State of the art

This section describes the basic computational methods for graph wavelet convolution, spatio-temporal graph definitions and prediction methods for spatio-temporal graphs.

A graph is generally represented as $\:A=(Q,E)$, where Q denotes the set of nodes of the graph A, and E denotes the set of edges. The most common computational representation of a graph is the adjacency matrix $\:M=\left\{{m}_{xy}\mid\:{q}_{x},{q}_{y}\right\}$. If only the connectivity between nodes is considered, $\:{m}_{xy}$ is simply taken as 0 or 1. If a further measure of the connection weights between nodes is needed, $\:{m}_{xy}$ is taken as the corresponding metric. Instead of using the adjacency matrix of the graph directly, spectral domain-based graph learning uses the Laplace matrix as an input to the graph structure.

Definition 1

(Graph Laplacian Matrix) Given an undirected graph A and its adjacency matrix M, the Laplacian matrix $L \in \mathbb{R}^{t \times t}$ of the specification of the graph A is denoted as:

$$\:L={X}_{t}-{D}^{-1/2}M{D}^{1/2}$$

(1)

Where D denotes the degree matrix of the graph A; $\:{D}_{xy}=\sum\:_{y}\:{M}_{xy}$ ; $\:{X}_{t}\in\:{\mathbb{R}}^{t\times\:t}$ is the unit matrix. The real symmetry property of the Laplace matrix L gives it standard nonnegative orthogonal eigenvectors $\:P=\left({p}_{1},{p}_{2},\cdots\:,{p}_{t}\right)\in\:{\mathbb{R}}^{t\times\:t}$. Each eigenvector corresponds to its nonnegative real eigenvalue $\:{\left\{{\lambda\:}_{l}\right\}}_{l=1}^{t}$, which is better able to express the structure of the graph, and thus the Laplace matrices are more often used to express the structure of the graph in graph learning.

Definition 2

(Graph Wavelet Transform) Given a set of wavelet bases $\psi_s = (\psi_{s1},\psi_{s2}, \ldots , \psi_{st})$. Where $\psi_{sx}$ denotes a signal diffused from node x to the graph; s is a hyperparameter that plays a scaling role. Then $\psi_{s}$ is expressed as follows.

$$\:{\psi\:}_{s}=P{A}_{s}{P}^{N}$$

(2)

Where P denotes the eigenvector; $\:{A}_{s}=dig\left(a\left(s{\lambda\:}_{1}\right),a\left(s{\lambda\:}_{2}\right),\cdots\:,\right.\left.a\left(s{\lambda\:}_{t}\right)\right)$ is a sparse diagonal array $\:a\left(s{\lambda\:}_{x}\right)={e}^{s{\lambda\:}_{x}}$. Based on Definition 2 the graph wavelet convolution operator can be constructed.

Definition 3

(Graph Wavelet Convolution Operator) Given a wavelet basis group $\psi_{s}$ and let the convolution kernel be θ, the graph wavelet convolution operation is denoted as $i *_A$ for an input signal $i \in \mathbb{R}^t$ and defined as follows.

$$\:i{*}_{A}\varTheta\:={\psi\:}_{s}\left(\left({\psi\:}_{s}^{-1}\chi\:\right)\odot\:\left({\psi\:}_{s}^{-1}\varTheta\:\right)\right)$$

(3)

Where ⊙ denotes the Hadamard product.

Setting $\:{a}_{\theta\:}={\psi\:}_{s}^{-1}{\Theta\:}$, the spectrogram convolution of a signal $\:i\in\:{\mathbb{R}}^{t}$ after filtering the convolution kernel $\:{a}_{\theta\:}$ can be equivalently expressed as:

$$\:i{*}_{A}\varTheta\:={\psi\:}_{s}{a}_{\theta\:}{\psi\:}_{S}^{-1}$$

(4)

Where$\:\:{\psi\:}_{s}=P{A}_{s}{P}^{\text{N}}=\left({\psi\:}_{s1},{\psi\:}_{s2},\cdots\:,{\psi\:}_{st}\right)$; $\:{\psi\:}_{s}^{-1}=\left({\psi\:}_{s1}{\:}^{*},{\psi\:}_{s2}{\:}^{*},\cdots\:,\right.\left.{\psi\:}_{st}{\:}^{*}\right)$ is the inverse transformation matrix of $\:{\psi\:}_{s}$.

In simple terms, a spatio-temporal graph consists of multiple graphs gathered over a finite time series. A spatio-temporal graph relies on the graph structure to reflect the spatial relationships of the nodes in the graph, while the feature data of the graph nodes change over time.

Definition 4

(Spatio-temporal graph) Given a time sequence N, the set of sequence graphs $\{ A^{n} | n \in N \}$ appearing in time order in N is called a sequence of spatio-temporal graphs over N. Further, for an t-node graph structure, the set of sequence graphs is denoted as $\{A^{n-B+1}, \cdots ,A^{n} \}$, assuming that the length of the history observation window is B, and n denotes the current moment. Each $A^{x}(x = n - B + 1, \cdots, n)$ is inscribed and involved in the spatial computation by a feature matrix as $Q_x \in \mathbb{R}^{t \times d}$, where d denotes the node feature dimension.

Definition 5

(Prediction of spatio-temporal graphs) Given a history window of length B, the eigenvalues of its corresponding nodes are denoted as $\{Q_{n-B+1}, \cdots ,Q^{n} \}$. Assuming that the prediction step is U, the spatio-temporal graph prediction is to use the history window data to get the prediction result for the future time period. The prediction value equation is:

$$\:{Q}_{n+1},{Q}_{n+2},\cdots\:,{Q}_{n+U}\leftarrow\:argmax\,{log}_{g}F\left({Q}_{n+1},\cdots\:,{Q}_{n+U}\mid\:{Q}_{n-B+1},\cdots\:,{Q}_{n}\right)$$

(5)

Extending prediction at the node feature set level to spatio-temporal prediction, Eq. (5) is expressed as:

$$\:{A}^{n+1},{A}^{n+2},\cdots\:,{A}^{n+U}\leftarrow\:argmax\,{log}_{g}F\left({A}^{n+1},\cdots\:,{A}^{n+U}\mid\:{A}^{n-B+1},\cdots\:,{A}^{n}\right)$$

(6)

Although Eqs. (5) and (6) are extremely similar, their implications are quite different.

Spatio-temporal graph prediction requires both temporal forecasting of node-level features and spatial assessment of inter-node connections and their impact on predictions. As depicted in Fig. 1, spatio-temporal graph prediction necessitates an evaluation of graph evolution across two dimensions: time and space. This figure demonstrates the progression of spatio-temporal graph prediction by highlighting the interactions between time and space dimensions. It visualizes how temporal forecasting at the node level and the spatial dependencies between nodes evolve over time, reflecting the dynamic nature of spatio-temporal data.

Fig. 1

Evolution of the spatio-temporal graph prediction model.

Methodology

This paper constructs a ST-GWNN model for data mining of timely spatio-temporal sequences in social media. The model directly considers spatio-temporal correlations across 2 dimensions, time and space, by fusing spatial graphs of multiple time steps (timely data points). These time steps, i.e., timely data points at a specific time, are used for information extraction by combining the spatial graphs for spatio-temporal association mining across both temporal and spatial dimensions.

In this section, we first provide an overview of the overall network architecture of the ST-GWNN model for spatio-temporal graph mining. Next, we introduce spatial-dependent feature extraction and temporal-dependent feature extraction separately. Finally, we explain the spatio-temporal convolutional block, which enables both spatial and temporal feature extraction.

ST-GWNN network architecture

The overall design architecture of ST-GWNN is shown in Fig. 2. It mainly includes three parts: input layer, spatio-temporal feature extraction layer and prediction output layer.

In the process of spatial feature extraction, the graph wavelet convolution layer is utilized to scale the channel up and down for scale compression and feature compression, facilitating the application of the bottleneck strategy. A spatio-temporal convolutional block typically consists of multiple temporal and graph wavelet convolutional layers, which are cross-stacked. The number and order of layers can be adjusted based on specific requirements. In this study, the model consists of “temporal convolution layer + graph wavelet convolution layer + temporal convolution layer " (TGT block for short). The enhancement of the localized expression of node features is accomplished by integrating techniques to improve the model’s expression effect and flexibility. Specifically, we adopt a method to capture local node features by considering the neighborhood information of each node within a defined radius. This process involves aggregating the features of neighboring nodes within the radius to generate localized representations of node features. Incorporating these localized representations enhances the model’s ability to capture spatial dependencies within the graph.

For temporal feature extraction, we design the model to stack causal convolutions through gated linear units to effectively capture the temporal dependencies of spatio-temporal sequence data. The process involves convolving the input sequence data with a causal convolution kernel, which aggregates a sequence of data points into a single data point, thereby capturing temporal dependencies within the data. Additionally, we utilize a gating mechanism, such as Sigmoid functions, to control the flow of information through the convolutional layers, enabling the model to focus on relevant temporal features while filtering out noise.

In order to fully capture the spatial and temporal correlation of spatio-temporal sequences, the graph wavelet convolution is nested with the causal convolution based on the gating mechanism in the spatio-temporal feature extraction process. This integration allows the model to simultaneously consider spatial and temporal dependencies within the data, facilitating more effective feature extraction and association mining across both temporal and spatial dimensions. The model uses two spatio-temporal convolutional blocks (TGT blocks). Each block consists of a temporal convolution, a graph wavelet convolution, and another temporal convolution. Together, these blocks mine spatio-temporal correlations across time and space by merging spatial graphs from multiple time steps.

Fig. 2

Architecture of the ST-GWNN model.

Temporal convolution layer design

Extracting time-dependent features is a key challenge in spatio-temporal graph modeling. In the modeling of time-series data, gating mechanism is considered to be the preferred solution, such as LSTM. Contemporary research within the field of digital signal processing and machine learning has begun to elucidate the underutilized potential of Convolutional Neural Networks (CNNs) in the domain of time-series analysis. Specifically, integrating CNNs with gating mechanisms significantly enhances model prediction capabilities for sequential data. This approach leverages the time-invariant feature extraction process of CNNs while employing gating to selectively retain or discard information based on its relevance to the prediction task, thereby capturing the temporal dynamics inherent in time-series data. In light of these findings, and to harness the strengths of CNNs for time-series prediction, this study introduces a temporal convolution layer that employs a causal convolution scheme. Causal convolution, characterized by its non-circular convolution operation, is strategically chosen to preserve the temporal integrity of the data, ensuring that the model only utilizes past observations to predict future outcomes. This method aligns with the causal structure of time-series data, where the temporal sequence is of paramount importance. By combining these techniques, the model can efficiently capture temporal dependencies within spatio-temporal sequence data, leading to more accurate predictions and feature extraction.

The model’s temporal convolutional layer, which employs causal convolution, is particularly suited for time-series prediction. This layer preserves the temporal integrity of the data, ensuring that the model only utilizes past observations to predict future outcomes. This causal structure aligns with the nature of time-series data in social media, where the sequence of events is crucial. The use of gated linear units in the temporal convolutional layer further enhances the model’s ability to capture temporal dependencies within the data, leading to more accurate predictions and feature extraction.

Definition 6

A causal convolution operation, denoted as $*_C$, involves a convolution kerne Γof size z. For a sequence of temporal data $I = \{Q_1, Q_2, \cdots ,Q_t \}$, a single causal convolution computes the following aggregation of z data points into a single output:

$$\:F\left(s\right)\leftarrow\:I{\text{*}}_{c}\varGamma\:\left(s\right)\leftarrow\:\sum\:_{x=0}^{z-1}\:{Q}_{s+x}\cdot\:{\gamma\:}_{x}$$

(7)

Where s indicates the current time step for computation. $\:F\left(s\right)$ is the resulting output for the computation at time step s. $\:{\gamma\:}_{x}$ represents the x-th element in the convolution kernel. This operation ensures that only past observations are utilized to predict future outcomes, aligning with the causal structure inherent in time-series data. In a sequence of length n, the convolution must be computed at least [t/z] times in the lowest layer. All computed values $\:F\left(s\right)$ are then used as inputs for subsequent layers. Causal Convolution ensures the temporal integrity of data in time-series analysis by basing predictions solely on past observations, a key requirement for maintaining sequence coherence. The size of the convolution kernel determines how many data points are aggregated for each computation, influencing the granularity of the temporal analysis.

In order to illustrate the implementation process of causal convolution more clearly, Fig. 3(a) gives an intuition of causal convolution. It aims to depict the process of how time-series data is transformed through causal convolution to capture temporal dependencies. In the figure, each node within the layers symbolizes a temporal data point in the input time-series. The arrangement of nodes reflects the sequential order of observations over time. The iteration of nodes across the layers illustrates the repeated application of the causal convolution operation. The figure starts with an initial input layer $\:{b}^{0}$ sequence of length t = 7. In order to obtain the predicted output of the output layer $\:{b}^{1}$ sequence of length t = 1, the output is given with a convolution kernel size of Γ = 2 × 1 for the input sequence data after passing through multiple hidden layers $\:\left({l}^{1},{l}^{2},\cdots\:,{l}^{5}\right)$. This is because in causal convolution, the sequence data with input length t is reduced to t - Γ + 1 after one causal convolution operation. It is then used as input for the next convolution operation and so on. Utilizing the combination of a simple gating mechanism and a convolutional neural network, the structure of the temporal convolutional layer of the ST-GWNN model is given in Fig. 3(b). A time window data of size $\:\left\{{Q}_{n}^{l},\cdots\:,{Q}_{n-B+1}^{l}\right\}$ is split into two ways into the respective causal convolutional networks. One path just goes through the Sigmoid function (denoted σ) to generate the output U. One other path goes through the residual linkage to generate the output V. This design not only avoids the inefficiency of causal convolution, but also reduces the risk of information loss through cross-layer linkage. The final output $\:\left\{{Q}_{n+1}^{l+1},\cdots\:,{Q}_{n+U}^{l+1}\right\}$ is the result of the computation of the product of the Hadamard products of U and V.

Fig. 3

Structure and causal convolution process of the temporal convolutional layer in the ST-GWNN model.

The temporal convolution layer performs temporal inference at the node level, analyzing each node individually. This requires considering the number of nodes (t) and their respective feature dimensions (d). Specifically, in Fig. 3(b), the inputs are represented (with d denoting the feature dimensions of the nodes), and the outputs are indicated.

The temporal convolution layer accomplishes temporal inference at the node level on a node-by-node basis, i.e., assuming the number of nodes and the feature dimensions of the nodes to be t and d, respectively. Specifically, in Fig. 3(b), the corresponding inputs are $\:I\in\:{\mathbb{R}}^{B\times\:t\times\:d}$ (with d being the feature dimensions of the nodes), and the outputs is $\:\in\:{\mathbb{R}}^{(B-2z-2)\times\:t\times\:d}$. Assuming a convolution kernel size of z, the length of the time series is reduced by z-1 units for each convolution implemented. Using a two-way causal convolution design, if B inputs are divided equally, the B inputs are reduced to 2×(B/2-z-1) = B–2z-2. It is clear that the temporal convolutional layer design of Fig. 3(b) has the advantage of high efficiency.

Graph wavelet convolution layer design

The temporal convolutional layer generalizes the node features over time at the node level but overlooks changes in the connectivity relationships (edges) of the nodes in the graph. Therefore, it also needs to complete spatial generalization with the assistance of graph neural network techniques.

Definitions 1 and 2 present the fundamental computational methods for graph wavelet convolution. Based on these definitions, for an input tensor I of dimensions $t\times u$ at layer, the output is depicted in Eq. (8).

$$\:{I}_{[:,y]}^{w+1}=b\left({\psi\:}_{s}\sum\:_{x=1}^{u}\:{F}_{x,y}^{w}{\psi\:}_{s}^{-1}{I}_{[:,x]}^{w}\right)$$

(8)

In the case of a two-layer graph convolution operation, the structure of its graph wavelet convolution operation is depicted in Fig. 4. In a neural network, input nodes initiate the process by receiving data. Hidden layer nodes, which are key to feature extraction, use weighted sums and ReLU activation functions to decide on signal transmission, with more nodes increasing complexity and learning power but also the risk of overfitting. ReLU nodes offer computational simplicity and gradient descent benefits. Output nodes generate the network’s final response, tailored to the problem type. Opting for two hidden layers enhances the network’s ability to learn complex patterns while balancing the risk of overfitting and computational demands, often chosen after experimental validation for its efficiency and adequacy for the problem’s complexity.

In this study, GWNN is used to extract the spatial topology hidden in the spatio-temporal data, for a tensor $\:{I}^{1}$ with input dimension $\:t\times\:u$ (taking $\:u=1$), the output after one GWNN can be obtained by Eq. (9).

$$\:{I}_{[:,y]}^{2}=ReLU\left({\psi\:}_{s}\sum\:_{x=1}^{u}\:{F}_{x,y}^{1}{\psi\:}_{s}^{-1}{I}_{[:,x]}^{1}\right)$$

(9)

Fig. 4

Graph wavelet convolution operation in the ST-GWNN model.

Design of spatio-temporal convolution block

To better capture the spatio-temporal dependency property, the design of the spatio-temporal convolution block directly considers the spatio-temporal correlation in two dimensions: time and space. It fuses the spatial graphs of multiple time steps (timely data points) together. The TGT block is chosen over the TG block because it integrates multi-dimensional features by stacking temporal and graph wavelet layers, improving the model’s sensitivity to both temporal and spatial dynamics. Adding normalization layers after each temporal convolution helps prevent overfitting and balances model complexity with generalization.

The TGT block is used twice to complete the spatio-temporal feature extraction. Utilizing the TGT block twice allows for a more thorough extraction of spatio-temporal features. The first TGT block captures initial temporal dynamics and spatial interactions, while the second TGT block further refines these features by capturing higher-order dependencies and complex patterns that may not be evident in the first pass. For the spatio-temporal graph sequence data $\:{I}^{l}\in\:{\mathbb{R}}^{B\times\:t\times\:{C}^{l}}$ input in layer l, it is input to layer $\:I+1$ after 2 TGT blocks. To prevent overfitting, a normalization layer is connected after each temporal convolution layer. If the size of the convolution kernel for the temporal convolution operation is $\:{Z}_{n}$, the node feature output $\:{Q}^{l+1}\in\:{\mathbb{R}}^{B-2\left({Z}_{n}-1\right)\times\:t\times\:{C}^{l+1}}$ of the l + 1th layer is computed as follows.

$$\:{Q}^{l+1}={\varGamma\:}_{1}^{l}{*}_{c}ReLU\left({\varTheta\:}^{l}{*}_{A}\left({\varGamma\:}_{0}^{l}{*}_{c}{Q}^{l}\right)\right)$$

(10)

Where $\:{\varGamma\:}_{0}^{l}$ and $\:{\varGamma\:}_{1}^{l}$ denote the dimensions of the time-gated convolutional kernels for the initial and subsequent convolutions, respectively, within the convolutional block at layer l. $\:{\varTheta\:}^{l}$ denotes the size of the convolutional kernel used for spatial topology extraction of the spatio-temporal map. $\:ReLU(\cdot\:)$ denotes the activation function.

The prediction output layer generates the final predicted map. It first takes the results from the feature extraction layer and passes them through an additional temporal convolutional layer, which then produces the single-step prediction output K. Then, a linear transformation with channel number c is performed on K before the final output is obtained. Where $\:m\in\:{\mathbb{R}}^{c}$ is the weight vector and h is the bias. The $\:{L}^{2}$ loss is utilized as the evaluation function of the ST-GWNN as shown in Eq. (11).

$$\:L\left(\widehat{Q},{M}_{\theta\:}\right)=\sum\:_{n}\:{||\widehat{Q}\left({Q}_{n-B+1},\cdots\:,{Q}_{n},{M}_{\theta\:}\right)-{Q}_{n+1}||}^{2}$$

(11)

Where$\:\:{M}_{\theta\:}$ is a trainable parameter; $\:{Q}_{n+1}$ represents the true observation; $\:\widehat{Q}(\cdot\:)$ represents the predicted output.

The graph wavelet transform within our ST-GWNN model offers a significant reduction in computational complexity compared to the Spectral CNN methods. It achieves this efficiency by eliminating the need for a full Eigen decomposition of the graph Laplacian, which can be computationally demanding. The graph wavelet transform operates with a more efficient complexity for processing graphs with a large number of nodes, allowing for a scalable approach to handling dense graphs. This method not only provides a sparse representation of spatial dependencies but also balances the inclusion of both local and global features. Consequently, the model’s efficiency is improved, making it well-suited for the analysis of large-scale social media data.

Result analysis and discussion

Data sets

In order to evaluate the effectiveness and generalization ability of the proposed model, this paper selects four relatively popular social media datasets for studying and analyzing the trends and patterns in user behavior, topic dissemination, and sentiment analysis.

A: Twitter dataset. Twitter is a typical social media platform, and its public dataset contains a large amount of time-series data, including tweets, retweets, and replies posted by users. The Twitter dataset is sourced from Twitter’s API and contains a large amount of time-series data, including tweets, retweets, and replies posted by users. The data encompasses a date range from January 2021 to December 2023.

B: Weibo dataset. Weibo is a Chinese social media platform that also provides rich time series data. The Weibo dataset is collected from the platform’s public API, covering posts from January 2021 to December 2023. This dataset can be used to analyze users’ opinions, emotional tendencies, and changes in hot topics.

C: Instagram dataset. The Instagram dataset, which includes photos and videos posted by users, as well as comments and interactions, is sourced from Instagram’s public API. It spans from January 2021 to December 2023, allowing for the analysis of changes in visual content over time.

D: YouTube dataset. The YouTube dataset contains information about the videos uploaded by users, including views, comments, and other engagement metrics. This dataset is obtained from the YouTube Data API, including data collected from January 2021 to December 2023.

Evaluation metrics

To measure the effectiveness of various methods for time series forecasting, this paper employs several evaluation metrics, including Mean Absolute Percentage Error (MAPE) and Root Mean Square Error (RMSE). These metrics are commonly used in the field of time series forecasting to assess model performance. MAPE measures the accuracy of a forecasting method by expressing the prediction error as a percentage. It is calculated using the equation:

$$\:\text{M}\text{A}\text{P}\text{E}=\frac{1}{n}\sum\:_{t=1}^{n}\:\left|\frac{{A}_{t}-{F}_{t}}{{A}_{t}}\right|\times\:100$$

(12)

RMSE measures the differences between predicted and observed values, giving a sense of how far off predictions are from actual outcomes. It is calculated as:

$$\:\text{R}\text{M}\text{S}\text{E}=\sqrt{\frac{1}{n}\sum\:_{t=1}^{n}\:{\left({A}_{t}-{F}_{t}\right)}^{2}}$$

(13)

Where: $\:{A}_{t}\:$is the actual value at time t, $\:{F}_{t}$​ is the forecasted value at time t, n is the number of observations.

In this study, the evaluated values for MAPE and RMSE are calculated as the mean and standard deviation of the performance metrics over 10 runs of the model, showcasing the variability and reliability of the model’s performance.

In the context of association mining, particularly within the scope of social media data analysis, we employ several key performance metrics to evaluate the effectiveness of our ST-GWNN model. These include Precision, Recall, and F1-score:

Precision measures the accuracy of the positive predictions made by our model. It is defined as:

$$\:\text{Precision\:}=\frac{TP}{TP+FP}$$

(14)

Where:$\:\:TP$ (True Positives) is the number of correct positive predictions. $\:FP$ (False Positives) is the number of incorrect positive predictions.

High precision indicates a low false positive rate, meaning the model is conservative in its positive predictions.

Recall, also known as sensitivity, evaluates the model’s ability to identify all relevant instances in the dataset. It is calculated as:

$$\:\text{Recall\:}=\frac{TP}{TP+FN}$$

(15)

Where: $\:FN$ (False Negatives) is the number of actual positives that were incorrectly predicted as negatives.

A high recall rate means that the model is thorough in identifying positive cases, even at the risk of including some false positives.

The F1-score is the harmonic mean of Precision and Recall, providing a single score that balances both metrics. It is particularly useful in cases where class distribution is imbalanced. The F1-score is defined as:

$$\:\text{F1-score\:}=2\times\:\frac{\text{\:Precision\:}\times\:\text{\:Recall\:}}{\text{\:Precision\:}+\text{\:Recall\:}}$$

(16)

The F1-score reaches its best value at 1 (perfect precision and recall) and its worst at 0.

These metrics are chosen for their ability to provide a comprehensive assessment of the model’s predictive performance in the context of association mining. Precision and Recall address different aspects of prediction accuracy, and the F1-score offers a balanced view that is particularly informative in cases of class imbalance, which is often encountered in real-world data.

Parameter sensitivity analysis

In this section, a parameter sensitivity analysis is conducted to evaluate and understand the strengths and weaknesses of the ST-GWNN model. This analysis fixes the architecture of the intermediate model and observes the impact of the overall performance by varying the time step. In time-series prediction, the time step represents different time granularity, e.g., daily, weekly. It reflects to some extent the amount of information that the neural network needs to memorize. Analyzing parameter sensitivity, especially the time step, is crucial for models like ST-GWNN. The time step directly impacts the model’s ability to capture temporal patterns: smaller steps provide finer detail, while larger steps offer a broader view. In the context of ST-GWNN’s complex spatiotemporal data, selecting the right time step is vital to avoid compromising model performance.

Currently, the majority of predictions conducted are one-step predictions, specifically forecasting the data for the following day. This constitutes a short-term prediction approach characterized by a small temporal granularity and high precision. As the time step increases, the temporal granularity expands, rendering the predictions more susceptible to external, unstable factors, consequently resulting in larger prediction errors. In this study, we assessed the predictive accuracy of the ST-GWNN model across various time step settings, namely 1-step, 3-step, 5-step, and 7-step predictions, employing the MAPE and RMSE as evaluation metrics. These results are visualized in Figs. 5 and 6. Notably, 1-step prediction pertains to forecasting the trend for the immediate next day, representing a short-term prediction. On the other hand, 3-step prediction signifies a trend spanning half a week, 5-step prediction indicates a one-week trend, while 7-step prediction generally encompasses the trend for the upcoming week and is often employed for long-term predictions. The error comparisons illustrated in Figs. 5 and 6 demonstrate that, across all social media datasets, short-term forecasts exhibit smaller errors compared to their long-term counterparts. This phenomenon aligns with common observations in the prediction domain. The underlying rationale is that long-term prediction data typically exhibit weaker correlations, coupled with larger time steps, thereby introducing increased instability factors and consequently leading to larger prediction errors. In pursuit of superior predictive performance, this study has opted for a 1-step time step for short-term prediction.

Fig. 5

Comparison of MAPE for different time steps.

Fig. 6

Comparison of RMSE for different time steps.

Figure 6 shows the RMSE for varying time steps (1-step, 3-step, 5-step, and 7-step) in the ST-GWNN model. The figure highlights how prediction errors grow as the prediction window increases, especially for long-term predictions (5-step and 7-step), emphasizing the importance of choosing appropriate time steps for accurate spatiotemporal forecasting in social media data. Based on the aforementioned experiments, it is evident that the crucial factor influencing the prediction outcomes of the ST-GWNN model is the time step.

Model interpretive analysis

Current end-to-end prediction models only utilize the target sequence for time series prediction. In contrast, this paper performs multi-feature extraction in both temporal and spatial domains through the ST-GWNN model. In order to verify the effectiveness of multi-feature extraction, the proposed model is compared with other multi-feature models (Model 1³⁰, Model 2³¹) as well as single-feature prediction models (Model 3³²). Model 1 utilizes a dual-stage attention mechanism and a Conv-LSTM architecture to capture spatio-temporal correlations. Model 2 employs wavelet transform coupled with a Long Short-Term Memory (LSTM) network to predict faults in electrical power grids. Model 3 analyzes the spatio-temporal distribution of data, such as the migration patterns of a specific species, using UAV-based photogrammetry and deep neural networks. Our ST-GWNN model differs from these comparison models in its approach to mining social media data. It integrates graph wavelet neural network techniques with a spatio-temporal convolutional block (TGT block) to effectively capture the intricate spatio-temporal dynamics inherent in social media datasets. Figure 7 provides a side-by-side comparison of prediction performance between the proposed ST-GWNN model, other multi-feature models (Model 1 and Model 2), and a single-feature model (Model 3). It demonstrates the effectiveness of the ST-GWNN’s spatio-temporal multi-feature extraction by showcasing tighter fitting curves for ST-GWNN predictions, reflecting better alignment with the actual data.

Fig. 7

Interpretation performance comparison chart.

To validate the method’s feasibility, we compare our model with the models from Model 1, Model 2, and Model 3 based on error results, as shown in Figs. 8 and 9.

Fig. 8

Error comparison of different models on MAPE.

Fig. 9

Error comparison of different models on RMSE.

From Fig. 8 it is possible to quickly assess which model has the lowest prediction error, with the ST-GWNN model showing the lowest MAPE among the comparison models. This suggests that the ST-GWNN model’s approach combining temporal and spatial features can produce more accurate predictions than models that rely on a single feature or different architectures. Figure 9 compares the RMSE of different models and shows that the ST-GWNN model consistently achieves the lowest RMSE over multiple time steps, reflecting superior prediction accuracy. The figure also confirms that the performance of the ST-GWNN model remains robust even as the prediction window increases.

The error analysis in Figs. 8 and 9 reveals that the prediction error of multi-feature models is smaller than that of single-feature models, indicating that multi-feature prediction can enhance the model’s performance. Additionally, the trend of MAPE and RMSE values shows that the prediction performance of the model starts to decrease with the increase in prediction time. However, compared to the other three models, the prediction error of this paper’s method is the lowest for predicting any time step. This is due to the fact that the ST-GWNN model designed in this paper utilizes graph wavelets to better extract the local information of the nodes, which improves the performance of the model node-level prediction. Furthermore, there is a reduction in computational complexity to some extent, thanks to the improved sparsity of the graph wavelet transform in both the spatial and spectral domains.

In addition, a comprehensive comparison of the proposed model with the other three models in terms of accuracy, precision, recall, and f1 scores was conducted. Statistical significance tests were performed using t-tests to determine whether the observed performance differences between the models were statistically significant. The experimental results are shown in Table 1.

Table 1 Performance comparison results on multiple metrics.

From the results in Table 1, we can observe that the ST-GWNN model proposed in this paper consistently outperforms the other compared models in terms of accuracy, precision, recall, and F1-score. These improvements are statistically significant (p < 0.05) according to the results of t-tests conducted for each metric. This indicates that the proposed model effectively captures the spatio-temporal correlations in social media data and provides superior predictive performance compared to the other data mining models.

In summary, we selected baseline models with diversity and relevance in order to fully assess the performance of the ST-GWNN model. The specific reasons for selecting these baseline models are as follows: (1) Model diversity: the baseline models we selected include different architectures and approaches (e.g., Model 1, Model 2, and Model 3), which enable us to evaluate the performance of the ST-GWNN model in multiple contexts. The different models employ their own unique feature extraction and prediction mechanisms when dealing with spatio-temporal data and user behavior, thus providing a valuable basis for comparison. (2) Relevance: the selected baseline models are all widely cited and validated in the field of social media data analytics and have good performance. This ensures fairness and relevance of the comparison. For example, Model 1 utilizes a two-stage attention mechanism to capture spatio-temporal correlation, while Model 2 combines wavelet transform and LSTM networks for fault prediction, which are similar to our proposed models in terms of objectives and techniques. (3) Comprehensiveness of evaluation metrics: based on different evaluation metrics (e.g., accuracy, precision, recall, and F1 score), we are able to have a more comprehensive understanding of the model’s performance in real scenarios. Our results show that ST-GWNN outperforms these baseline models in all metrics, further validating its effectiveness in social media data analysis. (4) Significance of the comparative analysis: by comparing with these baseline models, we are able to clearly demonstrate the advantages of the ST-GWNN model in capturing spatio-temporal correlations and handling complex user behaviors. These comparative results not only highlight the innovative aspects of the new model, but also provide new insights into the field of social media data analysis.

Model mining performance analysis

In order to verify the excellence of each model association mining results, the mining accuracy rate is used as a test metric, and the comparison results are obtained as shown in Table 2.

Table 2 Comparison of association mining accuracy of different models.

From the experimental data in Table 2, it can be seen that the average mining accuracy of the proposed model is 98.57%. The average mining accuracy of the model in literature³⁰ is 95.88%. The average mining accuracy of the model in literature³¹ is 92.24%. And the average mining accuracy of the model in literature³¹ is only 88.08%. By comparison, it can be seen that the mining accuracy of the proposed model is higher.

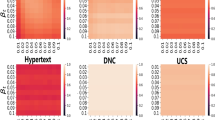
In order to further verify the application effect of different models, the different models are examined with the metric of association mining efficiency, and the specific experimental comparison results are shown in Fig. 10. The horizontal axis of Fig. 10 represents the number of test samples, while the vertical axis represents the efficiency of association rule mining. Each bar represents the mining efficiency of the corresponding model for a given number of test samples. The bars show the performance of each model in terms of association rule mining efficiency as the number of test samples increases. By comparing these bars with those of the ST-GWNN model, their performance under the same test conditions can be evaluated.

Fig. 10

Efficiency comparison of temporal sequence data mining for different models.

Analyzing the experimental data in Fig. 10, it can be seen that with the continuous increase of the number of test samples, the association rule mining efficiency of temporal sequence data of different models keeps changing. However, compared with the other three comparative models, the mining efficiency of this paper’s model is obviously higher, and all of them remain above 96%.

Ablation experiment analysis

To thoroughly assess the contributions of various components within our Spatio-Temporal Graph Wavelet Neural Network (ST-GWNN) model, we conducted a comprehensive ablation study. This analysis aimed to isolate the impact of key features, particularly the spatial feature extraction layer based on the Graph Wavelet Neural Network (GWNN), on the overall performance of our model. We systematically removed or disabled critical components and evaluated the resulting changes in performance across several metrics, including accuracy, precision, recall, F1 score, and mining accuracy (see Table 3).

Table 3 Ablation results.

From Table 3, it can be found that: the significant drop in performance when the graph wavelet transform is removed underscores its critical role in capturing spatial dependencies within social media data. Removing the temporal convolution layers leads to a considerable decrease in accuracy and mining accuracy. The performance drop when spatial convolution layers are removed indicates their importance in understanding the spatial relationships within the network. The slight decrease in performance when gated linear units are removed suggests that while they contribute to the model’s ability to filter out irrelevant information. The ablation study demonstrates that each component of the ST-GWNN model plays a significant role in its overall performance. The integration of these components is crucial for achieving superior results in spatio-temporal data mining tasks.

Practical applications and Case studies

The ST-GWNN model offers significant value across various domains, including targeted advertising, content recommendation, and crisis management. These applications highlight the model’s potential in analyzing social media data to assist businesses and policymakers in making more informed decisions. Below is a detailed case study in the field of targeted advertising that demonstrates the effectiveness of the ST-GWNN model in practical scenarios.

Case Study: A consumer electronics company is preparing to launch a new line of smartwatches with a focus on health and fitness tracking features. The company aims to target young professionals in urban areas who are actively engaged in social media discussions related to health and technology.

Application of ST-GWNN Model: By employing the ST-GWNN model, the company analyzed social media data to identify temporal patterns in user engagement and spatial clusters of users interested in health tech. The model’s graph wavelet transformation efficiently processed the complex, high-dimensional data, revealing that users in urban centers exhibit increased engagement during morning and evening commute hours.

Campaign Strategy: Utilizing the ST-GWNN model’s insights, the company decided to launch a series of targeted ads during the identified high-engagement periods. The ads highlighted the smartwatch’s health tracking capabilities and were geo-targeted to urban areas with the highest concentration of interested users.

Results: The campaign resulted in a 25% increase in click-through rates compared to previous, non-targeted campaigns. The ST-GWNN model’s ability to capture spatio-temporal dynamics led to more relevant ad placements, higher user engagement, and ultimately, a significant boost in conversion rates and ROI for the product launch.

Through this case study, we demonstrate how the ST-GWNN model can assist businesses in pinpointing their target audience more accurately, thereby enhancing the effectiveness of their advertising campaigns. The application of this model is not limited to the field of advertising; it can also be extended to other areas such as content recommendation and crisis management, providing data support and insights for a variety of decisions.

Conclusion

With the rapid evolution of the Internet and the pervasive use of social media platforms, users generate vast amounts of data, creating a dynamic online environment. These data contain valuable information that disseminates and circulates within the extensive network of social media, forming a foundation for comprehending and uncovering potential patterns within social media dynamics. Simultaneously, the sheer volume of this data presents new challenges for the methodologies employed in spatio-temporal analysis of social media. The continuous exploration and discovery of practical applications for social media data can effectively harness the latent societal value embedded within the data itself. To address this, this paper initiates its inquiry by examining the spatio-temporal distribution characteristics inherent in social media data. Building upon this examination, we introduce the ST-GWNN model. The ST-GWNN model operates in several key steps. Initially, it uses a graph wavelet neural network to understand the spatial relationships in spatio-temporal data by focusing on local node features. Subsequently, a time-gated convolutional layer extracts temporal feature information through causal convolution, leveraging gated linear units for enhancement. Furthermore, spatial maps from multiple time intervals (referred to as timely data points) are fused to discern correlation features across two dimensions: time and space. This approach enables the model to effectively mine complex spatio-temporal association mining within spatio-temporal sequences. Empirical results demonstrate that the proposed model exhibits superior accuracy and enhanced mining efficiency compared to existing classical data mining models. However, there is room for further improvement in the interpretability of our model. In future work, we will take the following steps to enhance the interpretability of the model: 1) Explore the use of feature importance assessment techniques, such as SHAP (SHapley Additive exPlanations) or LIME (Local Interpretable Model-agnostic Explanations), to quantify the contribution of each feature to the model’s predictions.2) Plan to develop visualization tools to intuitively display the model’s decision-making process at different levels, thus helping users understand how the model makes predictions from learned spatio-temporal features.