Introduction

As global climate change becomes increasingly severe, countries worldwide are ramping up their efforts to develop and utilize clean energy. Clean energy sources such as wind and solar power, known for their renewability and low pollution, have become crucial components of future energy transition strategies1. However, the randomness and volatility of clean energy pose significant challenges for grid scheduling. Traditional grid scheduling methods mainly rely on highly controllable energy sources like thermal and hydropower. These methods struggle to efficiently utilize clean energy while ensuring stable grid operation due to its inherent uncertainty2,3. Therefore, improving the utilization rate of clean energy without compromising grid safety has become a key issue in current grid scheduling optimization. The state grid Environmental, Social, and Governance (ESG) big data platform provides extensive data support and advanced technological tools for optimizing clean energy scheduling by collecting, storing, and analyzing various data within the power system. This platform integrates a wealth of historical and real-time data, including output data from wind and photovoltaic power, grid load demand data, and meteorological data, providing a comprehensive information foundation for scheduling optimization. However, data and platform support alone are insufficient; advanced optimization algorithms are needed to achieve truly efficient clean energy scheduling4,5.

To address these challenges, this work proposes an artificial intelligence (AI) empowered method based on the ESG big data platform to achieve multi-objective optimization of clean energy scheduling. The introduction of the ESG big data platform offers abundant data resources and powerful computational capabilities, enabling improvements in the scheduling decision-making process. This work deeply analyzes the complexity and uncertainty problems faced in clean energy scheduling within the current power system. It is found that applying AI technologies, particularly Particle Swarm Optimization (PSO) and the Deep Q-Network (DQN), to grid scheduling can significantly enhance scheduling efficiency and clean energy utilization. PSO, a heuristic search algorithm, is known for its simplicity, efficiency, and ease of implementation, showing great potential in solving optimization problems6. This work constructs a mathematical model for clean energy scheduling optimization. It sets the objective function to maximize clean energy utilization and minimize scheduling costs while considering grid safety and environmental constraints. The PSO algorithm quickly finds the optimal scheduling solution that meets these constraints. However, the high volatility of clean energy requires the scheduling system to have rapid response and dynamic adjustment capabilities7. To further enhance the adaptability and flexibility of the scheduling process, this work introduces DQN, a reinforcement learning-based algorithm that continuously learns and updates strategies through interaction with the environment8. The work designs a dual-layer architecture where DQN is responsible for adjusting the initially PSO-optimized scheduling plan based on real-time data during the actual scheduling process. This work aims to adapt to the instantaneous changes in demand and renewable energy output characteristics.

Literature review

Clean energy scheduling optimization has consistently been a hot research topic in the field of power systems. With the continuous increase in the installed capacity of clean energy, its randomness and volatility pose unprecedented challenges to grid scheduling. To address this issue, scholars have proposed various optimization methods and techniques. First, traditional Linear Programming (LP) and Mixed Integer Linear Programming (MILP) methods are widely used in clean energy scheduling optimization. Sarabadani et al.9 optimized the scheduling of wind and photovoltaic (PV) power using the MILP method. The findings showed that this approach had high computational efficiency in handling small-scale problems. However, LP and MILP methods face high computational complexity and long solving time when dealing with large-scale and nonlinear problems. Second, the application of metaheuristic algorithms in clean energy scheduling optimization has garnered extensive attention. PSO, Genetic Algorithm (GA), and Ant Colony Optimization (ACO) are widely applied in clean energy scheduling optimization due to their superior performance in complex optimization problems. Khan et al.10 applied GA to wind power scheduling optimization, significantly improving wind power utilization and economic benefits. Grisales-Noreña et al.11 optimized PV power scheduling using ACO, demonstrating that ACO performed well in solving nonlinear and multi-objective optimization problems.

With the development of AI technology, deep learning and reinforcement learning are gradually being applied to clean energy scheduling optimization. Zhai et al.12 proposed a wind power scheduling optimization method based on DQN, achieving intelligent wind power scheduling by simulating different load demands and wind power outputs. Li et al.13 applied Long Short-Term Memory (LSTM) networks to PV power forecasting and combined reinforcement learning to achieve optimal PV power scheduling. Additionally, hybrid optimization methods have shown great potential in clean energy scheduling optimization. Liu et al.14 proposed a hybrid optimization method based on PSO and GA, achieving collaborative scheduling of wind and PV power by combining the advantages of both algorithms. Kim et al.15 proposed a new scheduling optimization method by combining PSO with deep learning, which improved scheduling accuracy while reducing computational complexity.

Although the aforementioned research has made significant progress in clean energy scheduling optimization, there are still some shortcomings. First, most studies focus only on a single type of clean energy and lack consideration of the coordinated scheduling of multiple clean energy sources. Second, many studies fail to fully consider grid safety and environmental constraints, leading to limitations in the practical application of the optimization results. Finally, some studies lack robustness and adaptability in their algorithms, especially when faced with extreme weather conditions and drastic changes in load demand, resulting in suboptimal optimization performance. The innovation of this work lies in the combination of PSO and DQN, proposing a new multi-objective clean energy scheduling optimization method. By incorporating the ESG big data platform, this work not only enhances the data-driven capability of scheduling decision-making but also achieves rapid response and adaptation to instantaneous changes through a dual-layer architecture design. Compared to traditional methods, the proposed approach demonstrates significant advantages in improving clean energy utilization and reducing scheduling costs, while also exhibiting good robustness and adaptability under various conditions.

Research methodology

Architecture and functionality of the ESG big data platform

The ESG big data platform is a comprehensive environmental, social, and governance data management and analysis system. It is designed to provide extensive data support and decision-making assistance to the national power grid and related departments. The platform’s architecture is based on distributed computing and big data processing technologies, enabling efficient data collection, storage, processing, and analysis. Figure 1 illustrates the architecture of the ESG big data platform.

Fig. 1
figure 1

Architecture of the ESG big data platform.

Full size image

The ESG big data platform consists of four main components: the Data Collection Layer, Data Storage Layer, Data Processing Layer, and Application Layer. Data Collection Layer: This layer gathers real-time data from various sources such as sensors, smart devices, and energy management systems. Data includes clean energy generation, meteorological data, and electricity demand. Data Storage Layer: This layer utilizes distributed databases and big data storage technologies to efficiently store and retrieve vast amounts of data. Data Processing Layer: This layer applies advanced algorithms and models to clean, integrate, analyze, and mine data, providing essential support for scheduling optimization. Application Layer: This layer is the interface for users’ interaction with the platform, offering visualization tools and decision support systems for easy data querying, analysis, and scheduling decisions.

The ESG big data platform incorporates rich data resources spanning environmental monitoring, socio-economic data, and power system operational data. It encompasses traditional power system parameters and external factors influencing clean energy generation and utilization, such as weather forecasts, market supply-demand conditions, and regulatory policies. Comprehensive analysis across multiple dimensions enables the platform to provide more accurate and comprehensive scheduling information, laying the foundation for efficient clean energy utilization.

Additionally, the platform features robust computing capabilities with distributed computing frameworks and parallel processing technologies, enabling rapid processing and analysis of large-scale data. By integrating AI and machine learning algorithms, the platform conducts deep exploration of historical data to identify patterns and trends, thereby providing scientific insights for clean energy scheduling. For instance, analyzing historical weather and generation data enables the platform to forecast future clean energy outputs and optimize scheduling plans accordingly.

In terms of application potential in clean energy scheduling, the ESG big data platform offers strong support. It facilitates real-time monitoring and prediction of clean energy generation, aiding scheduling centers in promptly responding to generation fluctuations. Moreover, employing multi-objective optimization algorithms allows the platform to balance economic benefits and environmental impacts, devising optimal scheduling strategies to enhance clean energy utilization. Furthermore, by analyzing historical data, the platform identifies weaknesses in the scheduling process and proposes improvement recommendations, further enhancing scheduling efficiency and reliability.

Construction of multi-objective scheduling optimization model

In clean energy scheduling optimization, constructing a multi-objective scheduling optimization model is crucial. The design of this model needs to consider multiple factors to achieve efficient utilization of clean energy and maximize economic benefits16,17. Table 1 outlines the process for constructing the multi-objective scheduling optimization model:

Table 1 Process for constructing the multi-objective scheduling optimization model.
Full size table

First, the objective function design for clean energy scheduling optimization includes two primary objectives: maximizing clean energy utilization and minimizing scheduling costs. To achieve these objectives, the objective function is defined as follows (Eq. 1):

$$minimize\; f\left(x\right)=\alpha \cdot {f}_{1}\left(x\right)+\beta \cdot {f}_{2}\left(x\right)$$
(1)

\({f}_{1}\left(x\right)\) represents the scheduling costs, and \({f}_{2}\left(x\right)\) denotes the negative value of the clean energy utilization rate. The coefficients \({\upalpha}\) and \(\beta\) serve as weighting factors to balance the importance of these two objectives.

The clean energy utilization rate \({f}_{2}\left(x\right)\) is expressed as the ratio of clean energy generation to total generation, as shown in Eq. (2):

$${f}_{2}\left(x\right)=\frac{{E}_{clean}\left(x\right)}{{E}_{total}\left(x\right)}$$
(2)

\({E}_{clean}\left(x\right)\) represents the clean energy generation under scheduling plan \(x\), and \({E}_{total}\left(x\right)\) denotes the total generation. By maximizing this ratio, the efficiency of clean energy utilization can be enhanced, reducing reliance on fossil fuels and thereby lowering carbon emissions.

The scheduling costs \({f}_{1}\left(x\right)\) encompass generation costs and other related expenses incurred during the scheduling process, such as standby costs and start-up/shutdown costs. Its expression reads:

$${f}_{1}\left(x\right)=\sum_{i=1}^{N}{C}_{i}\cdot {P}_{i}\left(x\right)$$
(3)

\(N\) represents the number of generator units, \({C}_{i}\) denotes the unit generation cost of the \(i\)-th generator unit, and \({P}_{i}\left(x\right)\) represents the power output of the \(i\)-th generator unit under the scheduling plan \(x\).

During the optimization process, ensuring the safe and stable operation of the grid is essential. Therefore, the following grid safety constraints are established, as described in Eqs. (4) to (8).

$$\sum_{i=1}^{N}{P}_{i}\left(x\right)=D\left(x\right)+L\left(x\right)$$
(4)
$${P}_{i}^{min}\le {P}_{i}\left(x\right)\le {P}_{i}^{max}$$
(5)
$${R}_{clean}\ge {R}_{min}$$
(6)
$${E}_{carbon}\left(x\right)\le {E}_{limit}$$
(7)
$${P}_{pollutant}\left(x\right)\le {P}_{limit}$$
(8)

\(D\left(x\right)\) represents the load demand under scheduling plan \(\text{x}\), and \(L\left(x\right)\) denotes grid losses. \({P}_{i}^{min}\) and \({P}_{i}^{max}\) are the minimum and maximum power outputs of generator \(i\), respectively. \({R}_{clean}\) signifies the clean energy utilization rate, and \({R}_{min}\) is the minimum required clean energy utilization rate. Additionally, considering environmental constraints to minimize adverse impacts on the environment, Constraints 7 and 8 are established. \({E}_{carbon}\left(x\right)\) represents the carbon emissions under scheduling plan \(\text{x}\), and \({E}_{limit}\) is the carbon emission limit. \({P}_{pollutant}\left(x\right)\) denotes the pollutant emissions under scheduling plan \(x\), and \({P}_{limit}\) is the pollutant emission limit. Through the construction of the multi-objective scheduling optimization model described above, it is possible to maximize the use of clean energy and reduce scheduling costs while ensuring grid safety and environmental protection.

PSO optimization method

PSO is an optimization algorithm based on swarm intelligence, widely used in areas such as function optimization and neural network training. In the optimization of clean energy scheduling, PSO is favored for its simplicity, fast convergence speed, and effectiveness in solving multi-objective optimization problems. PSO simulates the foraging behavior of birds, achieving a global optimal solution search through information sharing among individuals (particles). Each particle represents a solution in the problem space, and its position is determined by its velocity, continuously updating within the search space18,19. Figure 2 illustrates the basic process of the PSO algorithm.

Fig. 2
figure 2

Basic process of the PSO algorithm.

Full size image

Updating the particle’s velocity and position is described by Eqs. (9) and (10):

$${v}_{i}\left(t+1\right)=\omega{v}_{i}\left(t\right)+{c}_{1}{r}_{1}\left({p}_{i}^{best}-{x}_{i}\left(t\right)\right)+{c}_{2}{r}_{2}\left({g}^{best}-{x}_{i}\left(t\right)\right)$$
(9)
$${x}_{i}\left(t+1\right)={x}_{i}\left(t\right)+{v}_{i}\left(t+1\right)$$
(10)

\({v}_{i}\left(t\right)\) represents the velocity of particle \(\text{i}\) at time \(t\), and \({x}_{i}\left(t\right)\) denotes the position of particle \(i\) at time \(t\). \({p}_{i}^{best}\) is the historical best position of particle \(i\), \({g}^{best}\) stands for the global best position, and \({\upomega}\) is the inertia weight. \({c}_{1}\) and \({c}_{2}\) are acceleration constants, and \({r}_{1}\) and \({r}_{2}\) are random numbers within the range [0, 1]. In clean energy scheduling optimization, PSO is used to find the optimal scheduling scheme to achieve multi-objective optimization. The specific application steps include: Particle Swarm Initialization: Initialize each particle’s position as a random scheduling scheme and velocity as a random value. Fitness Calculation: Compute the fitness value of each particle based on the objective function of clean energy scheduling optimization. Optimization Process: Incrementally approach the optimal scheduling scheme by updating particles’ velocities and positions. Result Output: Output the position of the particle with the highest fitness value as the optimal scheduling scheme. The fitness function is a critical measure of particle quality in PSO algorithms. In clean energy scheduling optimization, Eq. (3) defines the fitness function. With this fitness function design, PSO can effectively evaluate the merits of each scheduling scheme, guiding particles in the search for the optimal solution.

DQN optimization method

DQN is an algorithm that integrates deep learning with reinforcement learning, continuously improving decision strategies through interaction with the environment. In grid scheduling optimization, DQN dynamically adjusts scheduling schemes using real-time data, enhancing system responsiveness and adaptability. Built upon the Q-learning algorithm, DQN approximates the Q-value function using deep neural networks, overcoming the challenges of storing and computing Q-values in high-dimensional state spaces20,21. The DQN architecture comprises several key components: (1) The Input Layer: It receives state information from the environment, such as real-time electricity demand, clean energy generation capacity, meteorological conditions, etc. (2) The Hidden Layer: One or more hidden layers are utilized to extract feature representations from the state information, encompassing fully connected or convolutional layers. (3) The Output Layer: It outputs the Q-value estimates for each possible action. In the context of grid scheduling, actions include adjusting the generation ratios of various clean energies, initiating or halting certain power generation units, etc. Figure 3 illustrates the flow of the DQN algorithm.

Fig. 3
figure 3

DQN algorithm flow.

Full size image

In Fig. 3, the Q-value function \(Q(s,a)\) represents the expected reward obtained by taking action a in state s. DQN approximates the Q-value function using a deep neural network. The objective of DQN is to minimize the loss function, as shown in Eq. (11).

$$L\left( \theta \right) = {\mathbb{E}}_{{\left( {s,a,r,s^{\prime } } \right)}} \left[ {\left( {r + \gamma \underbrace {{max}}_{{a^{\prime } }}Q\left( {s^{\prime } ,a^{\prime } ;\theta ^{ - } } \right) - Q\left( {s,a;\theta } \right)} \right)^{2} } \right]$$
(11)

In Eq. (11), \(\theta\) represents the parameters of the Q-network, \({\theta }^{-}\) represents the parameters of the target network, r denotes the reward, and γ is the discount factor. Through experience replay, DQN randomly samples batches from an experience pool during training, breaking the correlation among samples and enhancing training effectiveness. Through reinforcement learning, DQN continuously adjusts scheduling strategies to learn the optimal scheduling policy, thereby enhancing the dynamic responsiveness and adaptability of grid scheduling.

Within the PSO-DQN joint scheduling optimization algorithm, the DQN model serves as the decision-making layer, interacting with the grid system. The DQN model receives real-time grid data from the main network and sends the scheduling decision results back to the main network for execution. The main network adjusts the operational status of power generation equipment according to the DQN model’s scheduling decisions to meet the load demands and optimization objectives of the grid. The main network then feeds back the grid state post-scheduling decision to the DQN model for further learning and optimization.

PSO-DQN joint scheduling optimization algorithm

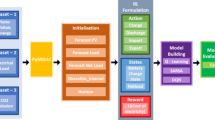
This work proposes a hybrid clean energy scheduling optimization algorithm that combines PSO and DQN to address the complex multi-objective optimization requirements in grid scheduling. Figure 4 illustrates the PSO-DQN joint scheduling optimization algorithm.

Fig. 4
figure 4

PSO-DQN joint scheduling optimization algorithm.

Full size image

Figure 4 illustrates the PSO-DQN joint scheduling optimization algorithm, where PSO handles initial scheduling optimization, and DQN dynamically adjusts during actual scheduling. The PSO algorithm first constructs a mathematical model for clean energy scheduling optimization and iteratively finds an initial optimal solution through particle swarm iterations. Subsequently, the DQN algorithm dynamically adjusts the preliminary optimization results of PSO based on real-time environmental feedback to cope with fluctuations in clean energy supply and changes in grid load demands. The objective of DQN is to optimize scheduling strategies by continuously updating the Q-value function, thereby enhancing the system’s dynamic responsiveness and robustness. This combined PSO-DQN scheduling optimization method not only leverages PSO’s global search capability but also utilizes DQN’s real-time adjustment feature to achieve adaptive optimization of scheduling strategies. Table 2 presents the pseudocode for the PSO-DQN joint scheduling optimization algorithm.

Table 2 The pseudocode for the PSO-DQN joint scheduling optimization algorithm.
Full size table

The upper-layer PSO algorithm plays the role of initial scheduling optimization in the dual-layer architecture. It generates a relatively stable scheduling plan based on historical data and forecasting models, aiming to maximize the utilization of clean energy and minimize scheduling costs. The DQN model, as the lower layer in the dual-layer architecture, is responsible for receiving real-time data (such as current clean energy generation capacity, load demand, etc.) during the actual scheduling process. Meanwhile, it dynamically adjusts the initial scheduling plan generated by the PSO based on this data. In the dual-layer architecture, the initial scheduling plan generated by the PSO algorithm is passed to the DQN model as an initial reference. The DQN model receives real-time data during the actual scheduling process and adjusts the initial plan based on this data. The adjustment results of the DQN model are fed back to the PSO algorithm as a reference for formulating future initial scheduling plans. This feedback mechanism helps the PSO algorithm generate scheduling plans that better align with actual needs in subsequent iterations.

Addressing the parameter tuning issue of the composite algorithm, the total number of particles (m) represents the number of particles in the algorithm. It is generally determined based on the scale and complexity of the problem, with this study setting it to 100. Acceleration factors (c1 and c2) are parameters that represent the influence of individual and global optima on particle velocity, with this study setting them to 2.05. The inertia weight (w) indicates the degree to which the particle’s current velocity affects the next velocity, used to control the convergence speed and search precision of the algorithm. The initial value is set to 0.9 and the final value is 0.4. The initial learning rate of the algorithm can be set to 0.001; the discount factor (γ) is 0.95 to emphasize the importance of future rewards. Results of single parameter variation based on sensitivity analysis are presented in Table 3.

Table 3 Variation results of a single parameter based on sensitivity analysis.
Full size table

Design of simulation experiment

This experiment aims to validate the effectiveness of the proposed PSO-DQN-based optimization method for clean energy scheduling through the State Grid ESG big data platform. The experimental data is sourced from the State Grid ESG big data platform, including real-time data from clean energy power stations (such as wind and solar power generation capacities), power grid load data, meteorological data, and user electricity consumption behavior data. The volume of data processed in the experiment is anticipated to reach the terabyte (TB) level, covering a long period of continuous data records to adequately reflect the randomness and volatility of clean energy.

Prior to the data being input into the model, necessary preprocessing steps such as data cleaning, denoising, and normalization are conducted to ensure data quality and the effectiveness of model training. Utilizing the real-time data collection capabilities of the big data platform, data are regularly collected from various sources and stored in a distributed file system. Data from different sources are integrated to form a unified data format and storage structure, facilitating subsequent processing and analysis.

The preprocessed data are divided into training, validation, and testing sets to ensure the effectiveness of model training and its generalization ability. The PSO-DQN model is trained using the training set data, and the model performance is enhanced by iteratively optimizing algorithm parameters. The real-time scheduling process is simulated on the validation and testing sets, using the DQN model to adjust the PSO scheduling plan based on real-time data, thus evaluating the model’s performance in practical applications.

Results

Performance of PSO-DQN method on different evaluation metrics

Figure 5 displays the comparison results of different scheduling methods in terms of clean energy utilization and scheduling costs. It reveals that the method combining PSO and DQN demonstrates significant advantages across various metrics. The clean energy utilization rate has improved from 62.4% in traditional methods to 87.7%, indicating a notable enhancement in the efficiency of clean energy utilization. Meanwhile, scheduling costs have decreased from 5.4 million RMB to 4.2 million RMB, a reduction of approximately 22%. There are also significant improvements in volatility and scheduling response time, indicating that this method is more stable and efficient in handling complex scheduling tasks.

Fig. 5
figure 5

Comparison of different scheduling methods in clean energy utilization and scheduling costs.

Full size image

Performance under different load demand conditions

Figure 6 presents the comparison results of clean energy utilization rates and scheduling costs under different load demand conditions. As the load demand increases, the clean energy utilization rate gradually rises, reaching a peak of 88.6%. Scheduling costs also increase with the increase in load demand but remain overall at a relatively low level. The stability of volatility and scheduling response time indicates that this method exhibits good adaptability and stability under varying load demands.

Fig. 6
figure 6

Comparison of clean energy utilization rates and scheduling costs under different load demand conditions.

Full size image

Figure 7 shows the comparison results of scheduling costs and the response time under different clean energy supply conditions. It suggests that with the increase in clean energy supply, the clean energy utilization rate gradually improves, reaching a maximum of 88.6%. Scheduling costs, on the other hand, decrease gradually, reaching a minimum of 4 million RMB. The reduction in volatility and scheduling response time also decreases accordingly, indicating that under adequate clean energy supply conditions, this method can optimize scheduling more efficiently and enhance overall system performance.

Fig. 7
figure 7

Comparison of scheduling costs and response time under different clean energy supply conditions.

Full size image

Adaptability to clean energy variability

Figure 8 reveals the performance in clean energy utilization rates and scheduling costs during different time periods. The clean energy utilization rate during peak hours is 86.8%, while it reaches 88.2% during off-peak hours and 87.5% during low-demand periods. During nighttime, the utilization rate is 88.1%. Scheduling costs show a consistent decreasing trend across different time periods. The stability in volatility and scheduling response time indicates that this method maintains efficient and stable scheduling performance throughout various time periods.

Fig. 8
figure 8

Performance of clean energy utilization rate and scheduling costs in different periods.

Full size image

Figure 9 illustrates a performance comparison of various scheduling algorithms under conditions of high clean energy variability. The PSO-DQN method achieves an 85.8% utilization rate of clean energy, significantly higher than the traditional method’s 60.3%. The scheduling cost is reduced from the traditional method’s 5.6 million yuan to 4.5 million yuan, with noticeable improvements in volatility and scheduling response time. Moreover, compared to the single advanced algorithm (Non-dominated Sorting Genetic Algorithm II (NSGA-II)) and the hybrid optimization algorithm (Genetic Algorithm-Reinforcement Learning (GA-RL)), performance enhancements are observed in terms of volatility and scheduling response time. This indicates that the method maintains efficient and stable scheduling optimization performance even under conditions of high clean energy variability.

Fig. 9
figure 9

Performance comparison of different scheduling algorithms under high clean energy variability.

Full size image

Figure 10 demonstrates the proposed PSO-DQN algorithm’s convergence from the perspective of the reward function. It can be observed that the agent under DQN training gradually converges after 600 epochs, with a smaller fluctuation range and stronger stability post-convergence. The reward function curve reveals that DQN exhibits superior performance in terms of convergence stability and precision.

Fig. 10
figure 10

Reward function of scheduling strategy.

Full size image

Further, in the experiment, different communication delay times are set: 0ms (no delay), 50 ms, 100 ms, 200 ms, and 400 ms to simulate delay conditions under various communication network scenarios. The specific results are listed in Table 4. It can be found that as the communication delay increases, the generation time of scheduling instruction increases significantly. This is because the algorithm needs to wait for a longer time to receive complete grid state information, thereby affecting the speed of scheduling instruction generation. Communication delays have a negative impact on the execution efficiency of scheduling instructions. The longer the delay, the more likely the algorithm is to fail to fully consider the most recent grid state information when generating scheduling instructions, leading to a decline in scheduling effectiveness.

Table 4 Algorithm delay under different communication networks.
Full size table

Discussion

This work proposes and validates the effectiveness of the PSO-DQN joint scheduling optimization algorithm in clean energy scheduling. Compared with traditional scheduling methods and single PSO or DQN methods, the research results demonstrate significant advantages of the PSO-DQN joint approach across multiple metrics. This finding is consistent with the perspectives of Zeng et al.22 and Chraibi et al.23. Specific advantages include:

Improved clean energy utilization rate: the PSO-DQN joint method shows a substantial improvement in clean energy utilization rate. The findings indicate an increase from 62.4% with traditional methods to 87.7% using this approach. This improvement is primarily attributed to the synergistic effect of PSO and DQN algorithms. As noted by Nama et al.24, the PSO algorithm demonstrated strong global search capabilities in optimizing initial scheduling schemes. It establishes a solid foundation for subsequent scheduling processes by exploring a wide solution space to find optimal or near-optimal scheduling schemes. Meanwhile, the DQN algorithm dynamically adjusts scheduling strategies based on real-time data during actual operations, enabling rapid responses to changes in clean energy supply. Through this dual-layer optimization architecture, the system identifies efficient scheduling schemes at the outset and continuously adjusts and optimizes them during operation. It enables the system to adapt to fluctuations in clean energy supply, thus achieving more efficient utilization of clean energy. This collaborative optimization strategy not only enhances clean energy utilization but also significantly reduces energy wastage compared to traditional methods, highlighting the substantial potential of intelligent scheduling systems in energy management.

Significantly reduced scheduling cost: in terms of scheduling cost, the PSO-DQN method also demonstrates significant advantages, reducing the scheduling cost from 5.4 million RMB in traditional methods to 4.2 million RMB, a reduction of approximately 22%. This cost reduction is primarily attributed to the efficiency and precision of the PSO-DQN method in optimizing scheduling strategies. First, the PSO algorithm utilizes its global search capability to find an optimized initial scheduling plan, ensuring a relatively low-cost foundation at the start of scheduling. Then, the DQN algorithm dynamically analyzes and adjusts scheduling strategies in real-time during actual scheduling processes to cope with changing demands and supply conditions. It can further optimize scheduling plans and reduce unnecessary energy waste and cost expenditures. This dynamic adjustment mechanism allows the scheduling system to flexibly respond to various uncertainties in actual operations, avoiding the high costs associated with traditional methods due to lack of real-time adjustments. By combining global optimization from PSO and real-time adjustments from DQN, the PSO-DQN method significantly enhances the economic benefits of the scheduling system, proving its effectiveness and superiority in optimizing scheduling strategies. Moreover, this cost reduction not only improves overall economic efficiency but also provides strong support for further promotion and application of intelligent scheduling systems.

Improved system stability and response time: the PSO-DQN method also shows significant advantages. Research results indicate that this method significantly improves system stability and reduces response time when handling complex scheduling tasks. Specifically, the PSO algorithm establishes a foundation for stable system operation by finding the optimal scheduling plan through global search. Meanwhile, the DQN algorithm dynamically adjusts schedules based on real-time data during the scheduling process, promptly responding to changes in load demands and clean energy supply conditions. This dynamic adjustment mechanism enables the system to make optimal decisions quickly in the face of emergencies and fluctuations, thereby avoiding instability and resource waste issues. Through the collaborative efforts of PSO and DQN, the system maintains efficient operation in complex scheduling tasks and adjusts rapidly to changes in load demands and energy supply conditions, ensuring operational stability and efficiency. This enhancement in stability and rapid response capability demonstrates the advantages of the PSO-DQN method in practical applications, better meeting the needs of clean energy scheduling and ensuring reliability and efficiency under various operating conditions. Therefore, the PSO-DQN method not only excels in clean energy utilization and scheduling costs but also exhibits tremendous potential in enhancing system stability and response time in intelligent scheduling optimization.

In adapting to varying load demands and clean energy supply conditions, the PSO-DQN method demonstrates outstanding adaptability and robustness. Further analysis of its performance under different load demands and clean energy supply conditions shows that the PSO-DQN method maintains high clean energy utilization rates and low scheduling costs, whether facing increased load demands or enhanced clean energy supply. This exceptional performance is primarily due to the combination of the PSO algorithm’s global optimization capability and the DQN algorithm’s dynamic adjustment ability. The PSO algorithm identifies optimal solutions during the initial scheduling phase, laying a solid foundation for subsequent scheduling processes. Meanwhile, the DQN algorithm adjusts scheduling strategies in real-time based on current data, ensuring efficient system operation under diverse conditions. The system exhibits good adaptability and stability in handling fluctuations and response time, enabling the PSO-DQN method to effectively address challenges in complex and uncertain environments related to clean energy scheduling. This capability ensures stable operation and efficient energy utilization, showcasing the method’s broad potential for applications in clean energy scheduling optimization.

Thus, the PSO-DQN joint scheduling optimization algorithm proposed not only demonstrates excellent practical performance but also holds significant theoretical value. First, by integrating PSO and DQN, two distinct optimization strategies, the algorithm introduces a novel approach to intelligent scheduling optimization, expanding the application boundaries of intelligent optimization algorithms in energy scheduling. Second, through comprehensive experimental validation and comparative analysis, the work provides ample evidence supporting the superiority of the PSO-DQN method in enhancing clean energy utilization, reducing scheduling costs, improving system stability, and reducing response time. This lays a solid foundation for future research.

In terms of practical value, the PSO-DQN method significantly enhances the operational efficiency and economic benefits of clean energy scheduling systems. It increases clean energy utilization, reduces energy waste, and enhances economic efficiency by lowering scheduling costs. Moreover, the method’s improved system stability and rapid response capabilities allow it to better handle fluctuations in load demands and energy supply in practical applications, ensuring stable system operation. These successful practical applications not only demonstrate the utility of the PSO-DQN method but also provide robust support for further promotion and application of intelligent scheduling optimization systems.

Conclusion

This work demonstrates the significant advantages of combining PSO and DQN methods in optimizing clean energy scheduling. It not only improves clean energy utilization rates and reduces scheduling costs but also exhibits good adaptability and stability in handling different load demands, clean energy supply conditions, and periods. The adjustment results of the DQN model are fed back to the PSO algorithm as a reference for making an initial scheduling plan in the future. This feedback mechanism helps the PSO algorithm to generate more realistic scheduling plans in subsequent iterations. Particularly under conditions of high clean energy variability, this method effectively mitigates adverse impacts from fluctuations, significantly enhancing scheduling efficiency and system stability.

Although the PSO-DQN joint method proposed demonstrates significant advantages in clean energy scheduling optimization, several limitations should be noted. First, the method relies heavily on large quantities of high-quality real-time data. The accuracy and timeliness of data significantly impact the effectiveness of scheduling results. Noise or delays in data could potentially degrade the performance of scheduling solutions. Moreover, the computational complexity of the PSO-DQN method is high, especially when dealing with large-scale power grids and high-frequency scheduling, which may consume substantial computing resources and affect the real-time responsiveness of the system. Additionally, this work primarily relies on simulation data for validation, and while the results show good performance, real-world applications may encounter more unforeseen complexities and challenges. Particularly, during extreme weather events or emergencies, the system’s robustness and adaptability need further validation and enhancement.

Future research can enhance the performance and application scope of the PSO-DQN method in several ways. First, more advanced algorithms such as multi-objective optimization algorithms and hybrid intelligent algorithms can be introduced to further improve the optimization effectiveness and computational efficiency of scheduling solutions. Besides, integration with actual grid data can be strengthened to conduct larger-scale field tests and validations, ensuring the method’s feasibility and stability in practical applications. Moreover, with the development of electricity markets and the increasing proportion of clean energy, future scheduling optimizations need to consider not only economic benefits and clean energy utilization rates but also carbon emissions and environmental requirements. It can help to construct more holistic and sustainable scheduling optimization models. Lastly, the application of the PSO-DQN method in other fields such as intelligent transportation and smart manufacturing can be explored. This can facilitate cross-domain intelligent scheduling optimization, providing insights and references for optimizing scheduling in more complex systems.