Forecasting dengue in Bangladesh using meteorological variables with a novel feature selection approach

Abstract

Dengue, a mosquito-borne viral disease, continues to pose severe risks to public health and economic stability in tropical and subtropical regions, particularly in developing nations like Bangladesh. The necessity for advanced forecasting mechanisms has never been more critical to enhance the effectiveness of vector control strategies and resource allocations. This study formulates a dynamic data pipeline to forecast dengue incidence based on 13 meteorological variables using a suite of state-of-the-art machine learning models and custom features engineering, achieving an accuracy of 84.02%, marking a substantial improvement over existing studies. A novel wrapper feature selection algorithm employing a custom objective function is proposed in this study, which significantly improves model accuracy by 12.63% and reduces the mean absolute percentage error by 70.82%. The custom objective function’s output can be transformed to quantify the contribution of each variable to the target variable’s variability, providing deeper insights into the workings of black box models. The study concludes that relative humidity is redundant in predicting dengue infection, while meteorological factors exhibit more significant short-term impacts compared to long-term and immediate impacts. Sunshine (hours) emerges as the meteorological factor with the most immediate impact, whereas precipitation is the most impactful predictor over both short-term (8-month lag) and long-term (26–30-month lag) periods. Forecasts for 2024 using the best-performing model predict a rise in dengue cases starting in May, peaking at 24,000 cases per month by August and persisting at high levels through October before declining to half by year-end. These findings offer critical insights into temporal climate effects on dengue transmission, aiding the development of effective forecasting systems.

Introduction

Dengue fever (DF), an acute viral illness caused by DENV virus, transmitted by mosquitoes, is prevalent in tropical and subtropical areas, affecting between 100 to 400 million people annually¹. Clinical symptoms of include nausea, vomiting, rash, and body aches, with severe cases potentially leading to plasma leakage, circulatory failure, or even death, as seen in dengue shock syndrome². Currently, treatment is primarily supportive, with no effective cure available³. The development of a dengue vaccine remains challenging due to the presence of four viral serotypes, making existing vaccines insufficient in halting disease transmission⁴. As a result, vector control, particularly the elimination of infected Aedes mosquitoes, is the most effective strategy for preventing the spread of dengue. However, traditional vector control methods are resource-intensive and economically burdensome. To optimize resource use, early forecasting of dengue cases could enable targeted interventions, such as deploying mosquito traps or utilizing Wolbachia-Aedes suppression technology⁵.

The intricate relationship between epidemiological and environmental factors makes it challenging to fully comprehend the long-term trends of dengue, hindering our ability to accurately predict disease incidence. Outbreaks often exhibit seasonal variations in specific regions, influenced by factors such as the population’s immunological and demographic composition, as well as environmental and weather conditions.

Previous studies have explored the relationships between meteorological factors, such as weather patterns, and DF incidence in Bangladesh and other affected countries^{6,7,8,9,10,11,12,13,14,15}. These investigations are crucial for developing effective DF forecasting models. Many studies have identified a positive correlation between precipitation and DF, with a lag of 0–3 months between periods of heavy rainfall and subsequent increases in case numbers^6,7,8,9,10. However, some research found no significant correlation^11,12 or even a negative association with a 2-month lag¹³. Consistently, minimum temperature was reported to be positively correlate with DF incidence at 1–2 month lags^{9,11,13,14,15}, and average monthly or weekly temperature showed positive correlations at 0–2.5 month lags in some studies^6,7,8,10, though others found no significant association¹². While temperature and rainfall were the most frequently analysed variables, other factors such as humidity, evaporation, sunshine hours, wind speed, and El Niño events were also examined. Relative humidity was found to be both positively^8,9,10,13 and negatively correlated¹² with DF, depending on the study, but when lagged by 1–3 months, it was consistently reported as positively correlated^9,13. Sunshine hours were variably reported as correlated¹² or inversely correlated^8,15 with DF incidence, while wind speed was inversely associated¹³ with DF cases for the same month. Additionally, average evaporation¹² and El Niño events¹¹ were positively associated with DF in some studies. The frequent identification of significant associations between meteorological factors and DF incidence suggests their potential as predictors for forecasting, but the variability in findings indicates that these relationships may be location-specific.

A wide array of forecasting techniques has been employed to predict DF incidence using weather data, both in Bangladesh and globally. Notable examples include studies conducted in Malaysia¹⁶; China¹³; France¹⁷; Vietnam^8,9,18; Mexico¹⁹;and Thailand²⁰. These methods encompass a variety of statistical and machine learning approaches, such as Poisson regression models^21,22, hierarchical Bayesian models²³, autoregressive integrated moving average (ARIMA) and seasonal ARIMA models^{17,18,19,24,25}, support vector regression (SVR)^26,27,28,29, least absolute shrinkage and selection operator (LASSO) regression^26,30, artificial neural networks (ANNs)³⁰, back-propagation neural networks (BPNNs), gradient boosting machines (GBMs)^27,31, generalized additive models (GAMs)^14,27, and long short-term memory (LSTM) models^16,27. Commonly, these models incorporate temperature and rainfall as key variables, while other factors, including humidity^8,9, air and water pressure²⁷, wind speed¹⁸, altitude, urban land cover²³, enhanced vegetation index¹⁶, and data from nearby regions through population flow²⁷ or spatial autoregression of DF risk²³, are also considered.

Recent studies^32,33,34,35 underscore how ML approaches, such as decision trees, support vector machines, and ensemble methods, excel in capturing complex, non-linear relationships among predictors, offering robust adaptability to diverse datasets and changing conditions. Unlike stochastic or probabilistic modeling frameworks, which often require extensive assumptions about data distributions and suffer from reduced performance when such assumptions are violated, ML models are data-driven and inherently flexible^36,37. For instance, ensemble learning techniques like Random Forests and Gradient Boosting have shown superior predictive performance across various public health scenarios due to their ability to combine the strengths of multiple base learners³⁸. Furthermore, ML models, particularly when coupled with automated feature selection algorithms, streamline computational processes, reducing both model training time and error margins³⁹. This efficiency, coupled with their capacity to accommodate high-dimensional, multivariate data, demonstrates the transformative potential of ML algorithms in forecasting frameworks, positioning them as more versatile and effective alternatives to traditional stochastic approaches in addressing complex epidemiological challenges^32,33.

Along with the literatures discussed above which illustrates the development of literatures on DF prediction in terms of demographics studied, variable considered, technique implemented both in terms of national and international dimension; the following studies will provide a glimpse on the academic advancement of DF infection prediction for Bangladesh:

Karim et al.⁴⁰ developed a dengue detection model utilizing multiple linear regression, with retrospective validation performed on data from 2001, 2003, 2005, and 2008. The study utilized monthly data spanning 2000 to 2008, sourced from the Directorate General of Health Services (DGHS) and the Meteorological Department of Dhaka, Bangladesh. This dataset included both dengue case counts and climatic variables such as rainfall, maximum temperature, and relative humidity. Their findings indicated a significant correlation between climatic fluctuations and dengue transmission in Dhaka. The model demonstrated efficacy by explaining 61% of the variation in dengue cases and accurately predicting dengue outbreaks (defined as $\ge 200$ cases) with a high area under the ROC curve of 0.89. However, the study’s scope was limited to Dhaka, and the results may not be generalizable. Furthermore, the final model did not account for temporal dependencies in the dependent variable, exhibited poor predictive accuracy, and employed an outbreak definition that is not recognized by the World Health Organization (WHO)³¹.

Hossain et al.⁴¹ conducted an analysis of dengue incidence in Bangladesh from 2000 to 2018, utilizing a generalized linear model to explore the relationship between climatic variables including monthly minimum temperature, rainfall, and sunshine and dengue incidence before the dengue season. The study relied on meteorological and epidemiological records, employing rigorous methods such as variable selection and leave-one-out cross-validation to enhance model accuracy. The findings revealed complex interactions between climatic factors and dengue incidence, highlighting that minimum temperatures positively influenced cases in late winter (January to March) but had a negative effect in early summer (April to June). An optimal temperature range of 21–23$^{\circ }\hbox {C}$ was identified as conducive to mosquito proliferation, emphasizing the significance of climate variability in predicting dengue outbreaks. However, the study had several limitations. The exclusion of data from 2019, which saw the largest dengue outbreak in Bangladesh during the study period, could significantly affect the study’s outcomes. Additionally, the model did not account for temporal dependencies of the predictors or the dependent variable, thereby failing to capture the inherent temporal effects of the problem. The model, by its design, predicted the annual number of dengue cases based on the monthly frequency of meteorological variables, reducing the number of predictors from 228 to 19, which likely led to model over fitting. These limitations may affect the generalizability of the results, suggesting the need for further research to refine predictive models for dengue incidence in the region.

Dey et al.²⁸ presents a machine learning approach to predict dengue incidents in Bangladesh by utilizing a dataset that includes hospitalized patients, meteorological data of 11 cities of the country. The study employs Multiple Linear Regression (MLR) and Support Vector Regression (SVR) algorithms, achieving accuracies of 67% and 75%, respectively. The findings indicate a seasonal pattern in dengue cases, with peaks during the rainy season, particularly in Dhaka, the capital of Bangladesh . However, the study has several limitations, the reliance on a limited geographic area restricts the generalizability of the findings. The model’s accuracy, while promising, suggests room for improvement, limited consideration of meteorological variables(rainfall, average temperature, relative humidity) in comparison to contemporary literature may have limited the performance of the prediction model.

Mobin et al.²⁵ investigates the challenges of data scarcity and discontinuity in healthcare and epidemiological datasets. The study employs a novel data downscaling algorithm namely Mahadee Kamrujjaman Downscaling (MKD) algorithm a.k.a. Stochastic Bayesian Downscaling (SBD) algorithm based on the underlying distribution. The authors exhibits two case studies using MKD algorithm to analyze data from two epidemiological cases namely Dengue and COVID-19 to evaluate the accuracy of synthesized data against aggregated actual data. Key findings indicate that the synthesized data closely aligns with the original data in terms of trend, seasonality, and residuals. The study uses the monthly dengue data from 2010–2022 to forecast the future values using univariate SARIMA model to show a comparative analysis of forecast using monthly data and downscaled daily data which exhibits improved forecasting accuracy up to 72.76%. Although the study shows promising results, it did not considered meteorological variables or any other factor for that matter impacting the complex dynamic of this disease.

In this study, we adopt a multivariate time series analysis of DENV infection cases in Bangladesh, leveraging 13 meteorological variables and machine learning (ML) models to forecast future trends based on the monthly historic data of DENV infection from 2010 to 2023. In response to the critical DENV infection situation in Bangladesh, the study presents a comprehensive data pipeline, enabling dynamic forecasting with a panel of leading ML, Deep Neural Network (DNN) models for time series forecasting. A novel wrapper feature selection algorithm, based on a custom objective function, is introduced to optimize accuracy and explain the percentage of variability each feature contributes to the target variable which adds to the explain ability of any ML model especially which were considered black box model. Using this variability centric feature importance, we compare and contrast between the different categories

The novelty and contributions of this study to the existing body of literature are outlined as follows:

• 1. A novel feature selection algorithm, termed ‘Sequential Squeeze Feature Selection’ (SSFS), is introduced. This algorithm enhances forecasting accuracy by 12.63% and reduces the Mean Absolute Percentage Error (MAPE) by 70.82%, significantly advancing precision in DENV infection prediction.

• 2. The study leverages a multivariate time series framework to analyze DENV infection cases in Bangladesh, integrating 13 meteorological variables and machine learning (ML) models. By utilizing historical monthly data from 2010 to 2023, this approach achieves an 84.02% accuracy with the best-performing model, outperforming methods reported in current literature.

• 3. A comprehensive and scalable data pipeline is developed, enabling dynamic forecasting of DENV infections. This pipeline integrates advanced ML models to provide actionable insights, offering a transformative tool for epidemic forecasting and resource allocation.

The remaining segment of the paper is structured as follows. “Materials and methods” section discusses the materials and methods of the study which includes discussion on the study design and site, data sources and description, methodology of the study. “Result” presents the findings of our study. “Future scope of the study” section discusses the further avenues that can be explored in the scope of this study. “Conclusion” section finally presents the concluding discussion of the study.

Materials and methods

Study site

Bangladesh, located near the Bay of Bengal (Fig. 1), comprises a significant portion of the Bengal Delta, shaped by sediment deposits from the Ganges–Brahmaputra–Meghna (GBM) river system⁴². The GBM rivers, originating in the Himalayan and Indo-Burman mountains, carry the world’s largest sediment load and rank fourth in global water discharge volume^43,44. Geographically, Bangladesh extends from $20^{\circ }34'N$ to $26^{\circ }38'N$ and $88^{\circ }01'E$ to $92^{\circ }41'E$⁴⁵.

Figure 1

Köppen-Geiger classification of Bangladesh’s climatic zones⁴⁷.

Figure 2

Demographic density map of Bangladesh for the year 2022.

Figure 3

Heat map of Dengue infection in Bangladesh during 2023.

Figure 4

Heat map of Dengue infection in Bangladesh during 2019.

Figure 5

Heat map of Dengue infection in Bangladesh during 2021.

Figure 6

Heat map of Dengue infection in Bangladesh during 2022.

Situated along the Tropic of Cancer, Bangladesh has a humid tropical to subtropical climate, with warm temperatures, high humidity, and seasonal rainfall variability⁴⁶. The Köppen-Geiger classification identifies three climate zones: Temperate with a dry winter and hot summer (Cwa; Zone 1), Tropical monsoon (Am; Zone 2), and Tropical savannah (Aw; Zone 3)⁴⁷. Annual rainfall averages 2300 mm, ranging from 1500 mm in the west to over 4000 mm in the northeast⁴⁸, while mean temperatures range from 18–22$^{\circ }\hbox {C}$ in winter to 23–30$^{\circ }\hbox {C}$ in summer. Climate models project a temperature rise of $2.4^{\circ }\hbox {C}$ and a 9.7% increase in rainfall by the century’s end⁴⁹.

As of 2022, Bangladesh’s population is 172.95 million, with high concentrations in Dhaka and Chattogram (Fig. 2)⁵⁰. Population density diminishes in suburban areas, paralleling dengue fever patterns, which predominantly affect densely populated urban zones. Figures 3, 4, 5, and 6 illustrate dengue case distributions for 2019, 2021, and 2023, indicating higher incidence in urban regions.

Dengue has been a recurring issue in Bangladesh since the early 21st century. While relatively controlled in its initial decade, rapid urbanization, waterbody encroachments, and climate change have intensified outbreaks. In 2023, dengue cases surged to a record 321,179-the highest in two decades. This alarming trend underscores the urgent need for robust forecasting to guide investments and precautionary measures, optimizing responses to future dengue threats.

Data

The dengue data used for the study is collected from Directorate General of Health Services (DGHS)⁵¹ and Institute of Epidemiology, Disease Control and Research (IEDCR)⁵² which is the number of individuals infected in Bangladesh per month. The average monthly sunshine hours data is collected from Bangladesh Agricultural Research Council (BARC)⁵³ and the rest of the meteorological variables are collected from National Aeronautics and Space Administration (NASA)⁵⁴. The time granularity of the all the data used in this study in monthly and such has been chosen to avoid the massive data discontinuity of DENV data on daily scale for our study site. The time range of the data used in the project is from January, 2010 to December, 2023 which is 168 months of data. A detailed description fo the meteorological variables can be found in Table 1.

Technical specification

All the simulation of this paper are done using Python 3.11.1 and Scikit Learn 1.3.2. The technical specification of the computers used for the computation is presented in Table 5 of the additional information section.

Figure 7

Visual representation of feature importance and the percentage of accuracy of the model explained by the variable. The figure illustrates feature importance of top ten features based on our final model (Decision Tree) in (a) and the corresponding percentage of accuracy explained by each variable in (b). It is evident that, higher feature importance does not correlates to higher percentage of accuracy by each variable. Thus, it is not always a great idea to prune features based on the lowest rank of feature importance.

Figure 8

Metric comparison between hyper parameter tuned models on the test set. The figure depicts the metrics comparison between the hyper parameter tuned best models of each class chosen by five fold time series cross validation score using grid search method over the test set. Here, we have three error measures and an accuracy measure as the choice of metrics based on which it can be easily deduced that Decision Tree (DT) is the best performing model in terms of accuracy and the other error metrics.

Figure 9

Dengue variability explained by features of varying categories, window size, and lag size. The figure illustrates the comparative analysis of explanatory accuracy posed by different categories and sub-categories of data from the final dataset of the study. It is evident from (a) that, meteorological data holds the most explanatory power over the variability of the DENV infection of which lagged variants holds a lion share of this over the non-lagged variants as illustrated in (b). From (c) for the lagged variants, the short term lag size poses better explanatory ability over the long term lag in comparison. In case of target derived features, (d) depicts the rolling window features holds the majority of the explanatory power over the others and the most impactful window size for the features are 12, and 6 months as portrayed in (f). In terms of the statistical measure used for target derived features, standard deviation holds the most explanatory power over mean which is evident from (e).

Methodology

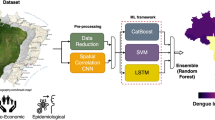
In light of the escalating dengue virus (DENV) outbreaks in Bangladesh in recent years, this study seeks to establish a robust forecasting pipeline, as illustrated in Fig. 10, tailored to address the growing challenge. Utilizing state-of-the-art machine learning models specifically designed for time series forecasting, the proposed framework aims to deliver highly accurate predictions of future outbreaks, primarily leveraging 13 meteorological variables. A comprehensive overview of the variables employed in this study, along with their descriptions, is provided in the “Data” subsection. This section further extends the discussion to encompass the data preprocessing steps, beginning with data cleaning and progressing through subsequent stages of the analysis.

Data cleaning

The data obtained from the aforementioned sources were mostly clean and did not contained any missing data points except for sunshine hours. There were a few missing values on the sunshine hour data which were imputed using the mean of the same month of the preceding three years.

Feature engineering

Feature engineering for time series data involves the creation of new features or the transformation of existing features to enhance the predictive power of machine learning models. This process is crucial as it helps in extracting the underlying patterns and temporal dependencies inherent in time series data. The feature engineering adopted in this paper is can be broadly classified as into three major groups which are discussed as follows:

• 1. Lagged Features:

  Lagged features, which are essentially past values of a time series, play a pivotal role in time series forecasting. They capture the inherent temporal dependencies within the data, enabling models to leverage historical patterns to predict future values. By including lagged features, we provide the model with crucial information about how the system evolves over time. But considering all possible lags for all the features may not necessarily be a great idea which in terms may decrease the accuracy of model given the existence of multiple redundant features at the cost of computational expense.

  An important step prior to using lagged features derived from other features is to pick features that has some degree of explanatory power over the target variable. Granger’s causality test can be invaluable tool in this regard. Granger’s causality test is a statistical hypothesis test used to determine whether one time series can predict another⁵⁵. Developed by Clive Granger, this test does not imply true causality but rather indicates whether past values of one time series contain useful information for forecasting another time series. The test is based on the idea that if time series X Granger-causes time series Y, then past values of X should provide statistically significant information about future values of Y, beyond what is already contained in the past values of Y alone⁵⁵. The null and the alternate hypothesis of the test are:

  • (a) $H_0:$ Time series X does not Granger-cause time series Y.

  • (b) $H_A:$ Time series X Granger-cause time series Y.

  Granger’s causality test is particularly useful for selecting which lagged features of a time series can help predict the target variable⁵⁶. This results in a more parsimonious model that generalizes better to unseen data.

  In order to capture the short term and long term impact of different features on the target variable (i.e. the number of DENV cases per month), we consider all lags $\in [1,36]\cap \mathbb {N}$ and conducted Granger’s causality test on the 13 meteorological features. For level of significance, $\alpha =0.05$, only 45 instances of the $13\text { features}\times 36\text { lags}=468$ instances showed p value$<\alpha$ i.e. 45 of such instances are appropriate features to predict the target variable. Detailed result of the conducted Granger’s causality test has been included in the table 6 of the additional information section. We consider these 45 instances as proper lagged features for predicting the target variable.

• 2. Target Derived Features:

  Target-derived features are features that are engineered using the target variable itself. These features are typically lagged versions of the target variable or transformations of the target variable over time, such as rolling and expanding window features, differences, or other statistical summaries, and seasonal decomposition. Including target-derived features often leads to improved predictive accuracy by providing the model with additional information about the historical behaviour of the target variable, enabling it to make more informed predictions. These features also enhance model interpretability by highlighting which past values of the target variable are most influential in predicting future values, offering valuable insights for domain experts and decision-makers^57,58. Additionally, features like rolling, expanding averages and differences are instrumental in handling seasonality and trends within the data. Rolling averages smooth out short-term fluctuations, making it easier to identify longer-term trends, while differencing can remove trends and make the series stationary⁵⁷.

  Seasonal decomposition techniques play a crucial role in enhancing time series forecasting models by separating data into distinct components like trend and seasonality, thereby improving forecasting accuracy⁵⁸. For instance, the Seasonal Decomposition for Human Occupancy Counting (SD-HOC) model utilizes seasonal-trend decomposition with moving average to transform data and employs different regression algorithms to predict human occupancy components, showcasing the effectiveness of seasonal decomposition in feature transformation⁵⁹. Incorporating seasonal decomposition as a feature in forecasting models can lead to more accurate predictions and better decision-making across various domains.

  The target derived this study adopts for analysis are:

  • Rolling Window Features: mean, and standard deviation.

  • Expanding Window Features: mean, and standard deviation.

  • Seasonal Decomposition Features: Trend, and seasonality.

  • Difference Feature: 1st difference of the target variable.

  • Seasonal Mean: Since, dengue exhibits an yearly cycle, hence we considered the mean of the target variable of the same month for the past years.

  In order to capture both the short and long term impact, the window that we considered on the monthly time frequency are: 3 (One quarter), 6 (Semi annual), 12 (Annual), 15 (Five Quarters), 18 (One and a half year).

• 3. Temporal Features:

  Temporal features are features that are extracted from the time component of the time series data. As the time granularity of the data used in the study is monthly, hence the temporal features used for the study are: year, month, and quarter.

The aforementioned feature engineering, particularly the creation of lagged features, has resulted in some missing values. Generally, machine learning algorithms are not well-equipped to manage these missing values. Consequently, we have opted to drop the missing values. Although this approach reduces the time length of our data frame, it enhances the dataset by increasing the number of features, thereby potentially improving the performance of our machine learning models.

The final dataset is obtained through the features engineering process as depicted in Fig. 10. The changes obtained in the final dataset by the feature engineering process is well illustrated in Table 2 in terms of time span, number of features and data points. The large number of features and data points using this process comes at the cost of fifteen months of time series and this necessary sacrifice shall make our upcoming workload easier for us.

Table 1 Description of the meteorological variables used for the study.

Table 2 A tabular representation of changes due to feature engineering.

Data preprocessing

Given that the dataset comprises features with varying magnitudes, we normalize it using a Min-Max scaler as in Eq. (1) to the range [0, 1]. This normalization ensures that no feature is given disproportionate importance due to its magnitude during the model training process.

$$\begin{aligned} x_{norm}=\displaystyle \frac{x-x_{min}}{x_{max}-x_{min}} \end{aligned}$$

(1)

The final dataset is split into three parts namely: 70% for training set, 10% for validation set, and remaining 20% for test set. The validation data kept for model optimization using our proposed novel method.

Model selection and hyper tuning

After the final dataset is ready, we use grid search over some predefined hyper parameter space for each of the models mentioned in Fig. 10. The best model hyper parameter for each model are selected based on cross validation score using five fold time series cross validation over the dataset. The model that we considered for the study are Decision Tree, K Nearest Neighbour (KNN), Support Vector Regressor (SVR), Random Forest, Gradient Boost, Extreme Gradient Boost (XGBoost).

We finally fit the hyper parameter tuned models to the train dataset and evaluate their performance on the test set to select the final model. The metrics we used for model evaluation are:

• Root Mean Square Error,

  $$\begin{aligned} \textrm{RMSE}=\sqrt{\displaystyle \frac{1}{n} \sum _{t=1}^n\left( y_t-\hat{y}_t\right) ^2} \end{aligned}$$

  (2)

• Mass Absolute Error,

  $$\begin{aligned} \textrm{MAE}=\displaystyle \frac{1}{n} \sum _{t=1}^n\left| y_t-\hat{y}_t\right| \end{aligned}$$

• Mean Absolute Percentage Error,

  $$\begin{aligned} \textrm{MAPE}=\displaystyle \frac{100 \%}{n} \sum _{t=1}^n\left| \displaystyle \frac{y_t-\hat{y}_t}{y_t}\right| \end{aligned}$$

  (3)

• R Squared,

  $$\begin{aligned} R^2=1-\displaystyle \frac{\displaystyle \sum _{t=1}^n\left( y_t-\hat{y}_t\right) ^2}{\displaystyle \sum _{t=1}^n\left( y_t-\bar{y}\right) ^2} \end{aligned}$$

  (4)

Sequential squeeze feature selection (SSFS)

Redundant features are variables that offer no new information beyond what is already provided by other features, potentially disrupting a model’s prediction accuracy. When features overlap in information, the model may become overly complex and prone to over fitting, performing well on training data but poorly on unseen data due to emphasizing noise and irrelevant patterns. Therefore, pruning redundant features is crucial. It simplifies the model, enhancing interpretability and reducing over fitting risk. Simplified models are easier to train, require less computational power, and have a lower chance of multicollinearity, which can destabilize the model and inflate coefficient variances.

Feature selection is the act of pruning the input data without essentially sacrificing the explainability of the data while effectively reduce noise or redundancy in order to provide a good prediction⁶⁰. Once a feature selection criterion is established, a procedure must be devised to identify the subset of useful features. Directly evaluating all possible feature subsets $(2^N)-1$ for a given dataset becomes an NP-hard problem as the number of features increases. Therefore, a suboptimal method must be employed to remove redundant features while maintaining computational tractability⁶⁰. Features selection methods can be broadly classified into filter, wrapper methods, and embedded method. Filter methods function as preprocessing steps, ranking features and selecting the highest-ranked ones for use in a predictive model. These methods are strictly dependent on the statistical properties and of the features hence often times are quite computationally efficient but is not often reflective of the models response to the addition/elimination of features from the dataset. In contrast, Wrapper methods treat the predictor as a black box and utilize its performance as the objective function to evaluate different subsets of variables. Given that evaluating all $2^N$ subsets is an NP-hard problem, these methods employ search algorithms such as Sequential Search algorithm, Genetic Algorithm, Particle Swarm Optimization to identify effective subsets^60,61. Wrapper methods can be divided into Sequential Selection Algorithms and Heuristic Search Algorithms⁶⁰. Sequential selection algorithms start with an empty or full set and iteratively add or remove features to maximize the objective function, stopping when the minimum number of features achieves the maximum objective value. Heuristic search algorithms evaluate various subsets to optimize the objective function, generating solutions by searching the space or solving the optimization problem. In case of the embedded methods, feature selection occurs as a by-product of the training process. This can be accomplished by incorporating constraints into the cost function of a predictive model, such as with Lasso⁶², or through algorithm-specific techniques, such as those used in random forests⁶³ and adaptive general regression neural networks⁶⁴. In this study we will concentrate on the sequential selection algorithms.

Several sequential selection algorithms such as Sequential Feature Selection (SFS), Sequential Backward Selection (SBS) algorithm, Plus-L-Minus-r search method, Sequential Floating Forward Selection (SFFS),for feature selection are available in the literature. The SFS algorithm begins with an empty set and iteratively adds the feature that maximizes the objective function, permanently including features that achieve the highest value of the objective function, until the desired number of features is reached⁶⁵. A SBS algorithm, similar to SFS, starts with the complete set of variables and iteratively removes the feature that causes the smallest decrease in predictor performance⁶⁶. Both methods are subject to the “nesting effect,” whereby discarded features in the “top down” search cannot be re-selected, and features once selected in the “bottom up” search cannot be later discarded. The Plus-L-Minus-r search method^65,67 aims to avoid nesting by adding $L$ variables and removing $r$ variables in each cycle until the desired subset of features is obtained. However, a significant limitation of this approach is the lack of a theoretical basis for determining the optimal values of $L$ and $r$ to achieve the best feature set. The Sequential Floating Forward Selection (SFFS) algorithm^65,66 offers greater flexibility than the basic Sequential Forward Selection (SFS) by incorporating a backtracking step. The algorithm begins similarly to SFS, adding one feature at a time based on the objective function. However, SFFS introduces an additional step where it excludes one feature at a time from the previously selected subset and evaluates the resulting subsets. If excluding a feature improves the objective function, the feature is removed, and the algorithm continues with the reduced subset. This process repeats until the desired number of features is selected or the required performance is achieved. A known limitation of the original SFFS algorithm is that after including and then excluding variables during backtracking, the resulting subset may be suboptimal than the one identified before backtracking⁶⁶.

One widely used wrapper method is Recursive Feature Elimination (RFE), which iteratively builds a model and removes the least important features based on their coefficients or feature importance until a certain number/percentage of features remains^56,68,69. However, a feature’s importance in a model does not always correlate with its impact on the model’s accuracy. A feature might significantly influence the model’s predictions without enhancing accuracy. For instance, an important feature in an over fitted model might increase variance without improving predictive power on unseen data. Conversely, a moderately important feature might stabilize the model and improve generalization. Figure 7 illustrates this issue, showing the feature importance of the top ten features for our final model and their corresponding contributions to model accuracy. The contribution of each variable in the model accuracy has been determined by our proposed feature selection approach. It is evident that feature importance does not necessarily correlate with higher accuracy. Therefore, relying solely on feature importance for feature selection may lead to erroneous pruning of necessary features, resulting in a substantial loss of accuracy until a desired number of features is reached. Therefore, it is crucial to employ accuracy-focused approaches, such as the SSFS algorithm proposed in this study, rather than relying on feature importance-centric methods. This ensures the achievement of optimal accuracy while minimizing the number of features used in unison with added explainability.

Again, feature importance or coefficients are not always available for all models, such as K-Nearest Neighbors or complex models like neural networks. A common practice is to use an interpretable model, such as a decision tree or Support Vector Machine (SVM) famously known as SVMRFE^56,68,69, to select features and then apply these selected features to more complex models. However, these methods might not be ideal for every generalized model. Decision trees assume that relationships between features and the target variable can be represented by a series of decision rules, which may not capture the complexities present in the data as effectively as more sophisticated models. SVMs focus on finding the optimal hyperplane to separate classes, which might not align with the criteria needed for other types of models. Therefore, while these models can provide initial insights, they might not illustrate the impact of each variable on the accuracy of more complex, non-linear models.

Table 3 Cross validation (CV) score of the five fold time series CV of the models.

Table 4 Impact of feature selection on model metrics.

Some of the major problems of the sequential methods used in the literature is that the most of the methods relies on the number of features on the final dataset or certain performance value to be decided beforehand which may subdue model performance as there are no theoretical development to deduce them beforehand. Nesting effect is also an issue for sequential feature selection schemes and finally the backtracking issue posed by SFFS. The performance of the sequential methods are also heavily reliant on the objective function used. Some of the commonly used objective/criterion function used are Mahalanobis distance⁶⁵, Leave One Out Cross Validation (LOOCV)⁶⁶.

Given the issues at hand, this study proposes an accuracy centric custom objective function in equation (5) whose output can be later transformed to explain what percentage of the model accuracy is explained by each variables. The study also proposes a novel feature selection algorithm namely ‘Sequential Squeeze Feature Selection (SSFS)’ which in essence is theoretical generalization of the SBS and SFS algorithm which in turn employs top down and bottom up approach to address the classical nesting problem posed by SFS, SBS and the backtracking problem posed by SFFS.

Let, $F=F_0=\{f_i:i\in \mathbb {N}_{n(F)}\}$ be the initial feature set or the feature set of $0^{th}$ iteration where n(F) is the cardinality of the feature set, F and $\mathbb {N}_m$ is the initial segment of the set of natural number which can be defined as $\mathbb {N}_m=\{1,2,3,\dots m\}$. $F_k=\{f_i:i\in \mathbb {N}_{n(F)-k}\}$ be the feature set in the $k^{th}$ iteration then $\forall i \in \mathbb {N}_{n(F)-k}$ and $\forall k \in \mathbb {N}_{n(F)-1}$, the proposed accuracy centric objective function for any feature $f_i$ on the $k^{th}$ iteration be defined as,

$$\begin{aligned} z_k(f_i)= {\left\{ \begin{array}{ll} A_{F_k}-A_{F_k-\{f_i\}} & \text {, for feature truncation cases where }f_i\in F_k\\ A_{F_k\cup \{f_i\}}-A_{F_k} & \text {, for feature inclusion cases where }f_i\in E_k \end{array}\right. } \end{aligned}$$

(5)

where, $A_{F_k}$ defines the accuracy of the ML model used on the feature space, $F_k$, $E_k$ denotes the set of eliminated features up to the $k^{th}$ iteration. Hence,based on the objective function in equation (5), we can coin the following mathematical definition of a redundant function,

Definition 1

(Redundant features) For $\epsilon >0$, a feature $f_i\in F$ is called a redundant feature iff

$$z_k(f_i)<\epsilon ,\quad \exists k\in \mathbb {N}_{n(F)-1}$$

One of the classical problem posed by sequential feature selection scheme is the nesting effect. The proposed SSFS algorithm aims to tackle this problem maintaining a omnidirectional movement of the feature $f_i$ between the feature space $F_k$ and eliminated feature set, $E_k$. As the algorithm depends on the mathematical definition of redundant feature hence unlike SFS, SBS; the number of features on the final dataset need not be decided priorly for the algorithm hence it depends entirely on the dataset and model itself. The algorithm uses top down and bottom up approach in a sequential fashion to to determine the final dataset hence the name ‘Sequential Squeeze Feature Selection’. A pseudocode of the proposed SSFS algorithm is included in Algorithm 1.

The algorithm works in a sequential fashion. Initially, the algorithm starts with feature truncation which continues until all the redundant features has been truncated using the objective function defined in equation (5). The algorithm backtracks the objective function value for each features and the set of eliminated features. Following this, the algorithm check for the features from the eliminated set if any of the eliminated features add any value to the current subset based on the predefined threshold. This continues in the aforementioned sequential manner until the value of the objective function for all the selected features meets the predefined threshold. The algorithm finally spits out the final set of features, $F^*$ and the final list of eliminated features, $E^*$.

The computational complexity of the SSFS algorithm is $O(m)+O(n\log n)$ where O(m) is the model complexity and the $O(n\log n)$ is the complexity to sort the feature importance of n featured dataset. If n become big then the corresponding model considered is also complex i.e. $O(m)>>O(n\log n)\text { for }n\rightarrow \infty$. Thus the computational complexity of the model is O(m) which is equivalent to the final model to be considered.

Algorithm 1

Sequential Squeeze Feature Selection (SSFS)

The output of the custom objective function we used can be transformed to project the percentage of accuracy of the model explained by each feature. Let, the SSFS executes for some finite iteration, N, then the final feature set, $F^*=F_N$, then the percentage of accuracy of the model explained by a feature, $f_i\in F_N$ can be defined as,

$$\begin{aligned} A_\%(f_i)=\displaystyle \frac{z_N(f_i)*100}{A_{F_N}\times \displaystyle \sum _{f_j\in F_N}z_N(f_j)}\% \end{aligned}$$

(6)

Result

Model selection

After the best models of each variant are selected based on their five fold time series cross validation score using grid search, we fit the best models to the training dataset and evaluate their performance on the test set to compare and contrast their performance on unseen data which is illustrated in Fig. 8. The figure illustrates the performance of the best hyper parameter tuned model of each type using the metrics of our choice. It is evident that from the figure that the Decision Tree (DT) is the best model in terms of both the accuracy and the error measures. Thus we will consider the DT model as “The Model” moving forward in this study. The cross validation score of the models are illustrated in Table 3 which shows that the results indicated consistent performance across all folds, with the decision tree model demonstrating stable accuracy and error metrics. These findings support the reliability of the model and align with the performance metrics reported for the test dataset as illustrated in Fig. 8.

Feature selection

We used our proposed feature selection approach, SSFS method for feature selection approach from the initial feature set, $F_0$ over the validation data. Prior to feature selection, the accuracy of the best model is 74.60%. We used SSFS to select the best feature subset, $F^*$. After the execution, the feature that was excluded was, ‘relative_humidity’, and the performance on $F^*$ is 84.01%. Thus, the feature selection scheme has eliminated one redundant feature which had boosted the accuracy by 12.63%, reduces the MAPE by 70.82% and the impact on the rest of the metrics are well illustrated in Table 4.

The proposed wrapper method and can be used for any ML or Deep learning model which will add to the explainability of the model outcome. The execution of the SSFS algorithm for the given model with 78 different features took only 0.8 seconds to executed.

Discussion based on feature importance

Based on the SSFS algorithm, we derive the feature importance in terms of accuracy of the model explained by each variable. Since the model accuracy is a measure of what percentage of variability of the target variable is explained by the model thus based on this the features importance of the variable can also be defined as the percentage of the variability of the DENV infection explained by the variables based on the model.

Based on the extensive feature engineering on the dataset that we have conducted the features can be broadly classified into 3 strata namely: meteorological, target derived and temporal. Initially, we want to observe how much variability of DENV infection can be explained by these three strata of features based on the best model. A graphical illustration of the query has been presented in Fig. 9a which illustrates that the majority variability (54.98%) of the DENV infection can be explained by the meteorological variables, followed by target derived features (40.98%) and the remaining (4.04%) can be explained by temporal variables.

We can take it further to see if the meteorological have higher immediate or lagged effect in explaining the variability of DENV infection which is also illustrated in the Fig. 9b. It has been observed that only 6.24% of DENV infection variability can be explained by immediate effect on the contrary, a staggering 48.74% of the variability can be explained by lagged effect. This helps us conclude that meteorological variable in case of DENV infection in Bangladesh have higher lagged effect in comparison to immediate impact.

Given that meteorological variables exhibit a more pronounced lagged effect compared to their immediate impact, it is pertinent to extend the scope of inquiry to explore the relative significance of these lagged effects over long-term versus short-term periods. A graphical representation of this analysis is provided in Fig. 9c. The graph clearly indicates that meteorological features have a greater impact in the short term compared to the long term. The most significant short-term lags are observed between 1 to 4 months, while the most influential long-term lags occur at 27, 26, 20, and 19 months, respectively.

On the other hand, target derived features exhibited higher explanatory power of the DENV variability. These are mainly comprised of rolling window, expanding window, seasonal decomposition, and difference features. Of these the rolling window features is the most impactful as illustrated in Fig. 9d. We can expand the idea to evaluate explanatory power of the rolling features varied by window size whose graphical illustration of which has been included in Fig. 9f. It illustrates the 12 month window length features holds the most explanatory power over the DENV infection variability followed by 6 month window size.

In target derived features, we mainly used two statistical measures namely mean and standard deviation (std) of which std holds the most explanatory power in comparison to the mean as illustrated in Fig. 9e.

Figure 10

The methodological work flow of the study. The figure depicts the methodological workflow of the study. We initially collect the data from DGHS, NASA, and BARC. Of the collected data, we clean off any additional data which are not conducive to our cause. Based on the clean data set we conduct necessary feature engineering and remove any missing value created in the process. which leaves us with the final dataset. At this stage, we conduct data preprocessing (i.e. scaling the data. doing train-test split etc.) necessary to make the dataset ready for ML model followed by the selection of the best model from the panel based on cross validation score over the some predefined hyper parameter space for the final dataset. Finally, based on our proposed novel feature selection algorithm, we weed out any redundant features for the model to fine tune the model performance to it’s optimal state. Based on the final model and optimal dataset, we generate forecast for the near future.

Figure 11

Radar plot of different categories of features. The figure illustrates the radar plot of different categories of features which illustrates that the standard deviation based features on an average hones better predictive ability of the DENV infection in Bangladesh over all other category of features.

Finally for categorical analysis, in gross comparison of different categories of features as illustrated in the radar plot of Fig. 11, we observe that standard deviation based features possess the best explanatory power over the mean based and lagged features derived from the raw data. This is because of higher variability observed for DENV infection cases over the last decade. In terms for window features, rolling window features have higher explanatory power over expanding window features which implies short term behaviour of the infection cases is good predictor of the future cases over the long term behaviour which suggest that the model was able to learn about the occurrence of recent shocks based on the training data.

Aside the categorical analysis, we can also analyse the explanatory power posed by each feature for the target variable. Prior to the individual feature analysis, we should analyse the distribution of the feature importance to develop an intuition of how the explanatory of DENV infection in distributed among the final feature set of seventy seven features. Figure 12 provides a graphical illustration of the distribution which illustrates the majority of the features have an explanatory power of the incident in the neighbourhood of one, very few in the neighbourhood of two and finally a handful around six and seven. This demonstrates the complexity of DENV infection scenario in Bangladesh which is not governed or dictated by some singular explanatory factor which makes it critical to be forecasted by classical approaches.

But to determine the major explanatory features for DENV infection in Bangladesh we can move to analysis of the top contribution features. The top ten features based on SSFS are illustrated in Fig. 13. It is evident from the figure that, the most contributing feature is the first difference of the target variable namely ‘Infected_diff’ which explain 6.73% of accuracy of the model. The meteorological variable in it’s lagged form comprises only 30% of the top ten features while 10% belongs to temporal variable and the staggering 60% belongs to the target derived features. This illustrates the importance of an effective feature engineering step which unravels complex pattern hidden within the data essentially boosting the performance of any ML or DNN model rather than relying on the raw data alone.

In order to explore the effect of meteorological features on predicting the dengue scenario, we initially explore the feature importance of the meteorological variables which is well illustrated in the Fig. 14. It is evident that the almost all the meteorological variables considered for the study have somewhat similar impact in explaining the accuracy of the model except for sunshine (hours). Thus, sunshine (hours) is the most impactful meteorological feature to predict the data variability posed by dengue in terms of instant effect.

The explanatory impact of lagged meteorological variables is illustrated in Fig. 15 which shows the top twenty of the total forty five lagged features selected using Granger’s causality test are all comprised of varying lags of precipitation. The most impactful lag of precipitation is 8 months and the second most impactful feature is sunshine (hours) with a lag of 2. The rest of the meteorological features have the most impact at a very short term lag which was also evident from previous categorical analysis of features. .It is evident from the Fig. 15 and also appendix that, the precipitation is the most impactful lagged meteorological which has not only short term impact like rest of the meteorological variables but also have long impact long term in dengue transmission and the impact can be as delayed as of 26 to 30 months which is more than that of two years.

Figure 12

Histogram of accuracy (%). The figure illustrates the frequency distribution of the variability explained by each features. Majority of the features has an explanatory power in the neighbourhood of one, very few in the neighbourhood of two and only a handful in the neighbourhood of six an seven which portraits that DENV infection is a complex phenomenon which is not explainable by a handful of factors rather the contribution of a lots of small factors which makes it notorious to be forecasted based on classical approaches.

Figure 13

Feature importance of the top ten features. The figure illustrates the top ten features in terms of percentage of accuracy explained by the model. The top contributing features is the first difference of the target variable. Of the top ten features, 60% are target derived features, 10% is temporal features, and the rest rest 30% are meteorological features.

Figure 14

Feature importance of the meteorological features. The figure illustrates the meteorological features in terms of percentage of accuracy explained by the model. Almost all the meteorological variables except for sunshine (hours) have similar impact on the accuracy of the model. Thus, we can say that sunshine (hours) is the most impactful meteorological features in terms of immediate effect.

The followings are the major takeaways on the DENV infection scenario of Bangladesh based on the feature importance analysis of the best fitted model:

• 1. Although relative humidity is traditionally considered a significant factor in the rapid spread of dengue in tropical countries, as noted in previous studies^27,28,70,71, our research indicates that it is a redundant feature for predicting dengue cases in Bangladesh across immediate, short-term, and long-term effects. This finding is supported by its removal as a redundant feature through the SSFS method and its lack of significant lag in the Granger causality test, as detailed in Table 6 of the additional information section.

• 2. The majority of the variability in DENV infection (54.98%) can be attributed to meteorological variables, followed by target-derived features, which account for 40.98%. The remaining 4.04% is explained by temporal variables. This distribution is illustrated in Fig. 9a.

• 3. The majority of the variability in DENV infection can be attributed to feature-engineered variables rather than raw features. As illustrated in Fig. 9a, b, only 6.24% of the variability in DENV infection, as explained by the model, is accounted for by raw, non-lagged features. In contrast, the remaining 93.76% is explained by feature-engineered variables. This underscores the critical importance of knowledge-driven feature engineering in the data pipeline when predicting complex real-world phenomena, such as DENV infection.

• 4. Meteorological factors associated with DENV transmission exhibit a significantly greater impact over both short and long-term periods, as opposed to their immediate effects. This distinction is clearly demonstrated in Fig. 9b.

• 5. Sunshine (hours) stands out as the meteorological variable with the most immediate effect when compared to other meteorological factors, as illustrated in Fig. 14.

• 6. Meteorological features exert a more substantial impact in the short term compared to the long term. The most significant short-term lags are observed between 1 to 4 months, while the most influential long-term lags occur at 27, 26, 20, and 19 months, respectively. This pattern is illustrated in Fig. 9c.

• 7. Target-derived features play a crucial role in explaining DENV variability, with rolling window features emerging as the most impactful. The effectiveness of these features is dependent on window size, as demonstrated in Fig. 9f, where a 12-month window length offers the greatest explanatory power, followed by a 6-month window, indicating that short-term behavior of infection cases is a better predictor of future trends. Additionally, standard deviation-based features consistently outperform mean-based and lagged features, likely due to the higher variability in DENV infection cases observed over the past decade, as illustrated in Fig. 11.

• 8. Figure 12 illustrates that most features have explanatory power near one, with fewer around two, and a small number near six and seven, highlighting the complexity of the DENV infection scenario in Bangladesh, which is not dominated by a single factor and challenges classical forecasting approaches.

• 9. The top ten features identified by SSFS, as shown in Fig. 13, reveal that target-derived features contribute 60%, with the first difference of the target variable, ‘Infected_diff’, explaining 6.73% of model accuracy, while lagged meteorological variables comprise 30%, and temporal variables account for 10%.

• 10. Figure 15 demonstrates that precipitation, particularly with an 8-month lag, is the most impactful lagged meteorological variable, with precipitation showing both short-term and long-term effects on dengue transmission, extending up to 26–30 months.

Forecast

Based on the previous feature engineering and data preprocessing techniques, we have also prepared our forecasting dataset for the year of 2024. For any data that we have no future data on like meteorological data, infection trend or seasonality, we considered it be the average of the same month for the last three years and the rest of the features are created from it based on previous feature engineering steps. Based on this data set and the optimal model, we have forecasted the DENV infection scenario of Bangladesh in 2024 as illustrated by the red lines in Fig. 16. The figure shows that the infection will start climbing from May and will peak at August and persists till October to figure of around 24 thousand cases per month and will be reduced to half by the end of the year. It also illustrates the model fit in the training and test phase. The model has performed in the test phase with 84.02% accuracy and the details on the rest of the matrices has been delineated in Table 4.

Figure 15

Feature importance of the top 20 lagged meteorological features. The figure illustrates the top twenty lagged meteorological features in terms of percentage of accuracy explained by the model. It is evident that, the category of lagged features is predominated by precipitation.

Figure 16

Forecast of 2024 based on monthly DENV data from Jul, 2012 to Dec, 2023. The figure illustrates the DENV infection forecast of 2024 based on the historic data of the last decade. The forecast suggest that the infection count will climb from May, reach its peak 2k thousand monthly cases in August which will sustain till October from it will decline to half it’s peak by the December of 2024. It also illustrates the model training and test fit. The model has performed on the test set with 84.02% accuracy and the details on the rest of the metrics can be found on Table 4.

Conclusion

This study employs a multivariate time series analysis of DENV cases in Bangladesh, leveraging meteorological variables and machine learning models to forecast future trends. In response to the critical DENV situation in Bangladesh, the study presents a comprehensive data pipeline, enabling dynamic forecasting with a panel of leading ML models for time series forecasting. A novel wrapper feature selection algorithm, based on a custom objective function, is introduced to optimize accuracy and explain the percentage of variability each feature contributes to the target variable. The decision tree model emerged as the most effective, achieving 84.02% accuracy during testing, representing a 12.63% improvement in accuracy and a 70.82% reduction in MAPE through the use of the SSFS method. Statistical tests and feature selection reveal that relative humidity is a redundant feature in predicting DENV infection in Bangladesh across immediate, short-term, and long-term impacts. The study identifies meteorological features as having a stronger short-term effect, with sunshine (hours) as the most immediate influential factor, precipitation with an 8-month lag as the most impactful lagged feature, and precipitation as the sole meteorological variable with both short- and long-term (26–30 months) effects on DENV transmission. The findings highlight the complexity of the DENV infection landscape in Bangladesh, which challenges traditional forecasting methods, and predict a worst-case scenario of 24,000 cases per month in 2024, persisting from August to October and gradually declining by December.

Bangladesh’s current dengue management suffers from a disconnect between data collection and vector control implementation, leading to suboptimal disease control and overburdened healthcare systems. To address this gap, a centralized disease control agency is proposed, integrating data-driven insights into coordinated action plans. By leveraging the forecasting pipeline developed in this study, this agency could optimize resource allocation, streamline vector control measures, and mitigate the seasonal strain on the healthcare system. Such a unified approach would significantly improve the nation’s capacity to manage DENV outbreaks and other epidemic diseases effectively.

Future scope of the study

To address data discontinuities in daily DENV infection reports in Bangladesh, the study adopts a monthly time granularity, which may reduce accuracy due to lower data volume. Recent advancements in downscaling algorithms, known to enhance classical forecasting models’ accuracy by up to 72.76%, could be explored to improve the performance of ML/DNN/Hybrid models. Additionally, while the novel SSFS feature selection scheme was applied exclusively to the Bangladesh Dengue dataset, further comparative studies with similar algorithms across different problems, models, and datasets would provide valuable insights into its broader applicability and effectiveness.