Introduction

Breast cancer (BC) is the most normal cancer in women when compared to others. According to the report of WHO, it is the fourth foremost reason for cancer death1. The histological score is an essential analytical factor in forecasting the determination of the BC. It is gained by utilizing the Nottingham Grading System (NGS) by evaluating three dissimilar cancer features: nuclear pleomorphism, tubule creation, and mitotic level2. According to the NGS, the mitotic rate delivers substantial analytical value for these three features. Therefore, mitosis recognition is vital in accurately valuing cancer analysis and ranking and forecasting treatment efficiency and existence3. In addition, the valuation of the mitotic rate is based on the accurate identification of MN in whole slide image (WSI)4. Such identification challenge is generally executed by pathologists optically, which is very complex, extremely flexible, intensive, and time-consuming. So, it is highly vital to improve an automatic computer-aided model for the classification of mitosis5. The MN visual identification by pathologists is a biased and time-consuming challenge with poor reproducibility owing to numerous tasks6. MN are hyper-chromatic substances with numerous morphological sizes and shapes. Furthermore, the existence of MN in a 10 HPF differs based on cancer grade and level. In aggressive cancers, generally, MN acts in small size with the highest rate and is non-differentiable. Accurately identifying MN relies upon pathologists’ knowledge and experience7. Object-level inter-observer research discloses pathologists’ differences on separate objects. The limits of physical workflow produce the necessity to mechanize the calculating of MN to enhance the pathologist’s conclusion. The histopathology digitalization and growth in medical image processing and machine learning (ML) techniques started a period of computer-aided pathology8. In this respect, dissimilar automatic methods could be developed, such as identifying cancerous tissues, biomarker identification, recognition of nuclei, and so on. Dissimilar models have been developed for MN identification in HIs depending on the detection, classification, and segmentation tasks9. Current models repeatedly oppressed data balancing plans like rotation, translation, and mirror imaging-based methods to enlarge the mitotic instances. Convolutional Neural Networks (CNNs) were attractive and well-known for image data classification and for learning noble feature representation. The feature learning capability of CNNs relies upon an image input representation and design of CNNs10. Enhancing feature pictures improves CNNs’ ability to discern features, and superior performance on classification challenges is attained.

This manuscript proposes the Coati Optimization Algorithm with Deep Learning-Driven Mitotic Nuclei Segmentation and Classification (COADL-MNSC) technique. The major aim of the COADL-MNSC technique is to utilize the DL model to segment and classify the mitotic nuclei (MN). In the preliminary stage, the COADL-MNSC approach implements median filtering (MF) for pre-processing. Besides, the COADL-MNSC approach utilizes the Hybrid Attention Fusion U-Net (HAU-UNet) model to segment the MN. Moreover, the capsule network (CapsNet) model is employed for the feature extraction method, and its hyperparameters are adjusted by utilizing the COA model. At last, the classification procedure is performed using the bidirectional long short-term memory (BiLSTM) model. Extensive simulations are performed under the MN image dataset to exhibit the excellent performance of the COADL-MNSC methodology. The key contribution of the COADL-MNSC methodology is listed below.

  • The COADL-MNSC model utilizes MF to enhance image quality, significantly mitigating noise and thereby enhancing the accuracy of subsequent segmentation. This preprocessing step is significant for ensuring that the segmentation process can efficiently distinguish between mitotic nuclei and complex backgrounds. As a result, it lays a solid foundation for more precise analysis in later stages.

  • The HAU-UNet model is implemented to improve the segmentation of mitotic nuclei by incorporating attention mechanisms that emphasize relevant features while effectually suppressing distracting background data. This approach results in more precise delineation of nuclei, facilitating improved detection and analysis. By concentrating on critical areas of the image, it improves the overall performance of the method in recognizing mitotic events.

  • Employing CapsNet model substantially improves the feature extraction capabilities of the technique, allowing it to efficiently capture intrinsic spatial hierarchies within the data. This enhanced understanding of spatial relationships results in an improved discrimination of mitotic nuclei characteristics. As a result, the model can more precisely detect and classify mitotic events, enhancing its overall performance in image analysis.

  • The utilization of the COA model for hyperparameter optimization crucially improves the performance and robustness of both segmentation and classification processes. By fine-tuning these parameters, the model attains enhanced accuracy and reliability in detecting mitotic nuclei. This strategic adjustment results in more effectual learning and better generalization to diverse datasets.

  • The novel integration of HAU-UNet with capsule networks and hyperparameter optimization presents a distinctive approach for precisely segmenting and classifying mitotic nuclei in intrinsic imaging conditions. This integration not only improves the capability of the model to concentrate on relevant features while minimizing background noise but also allows for capturing complex spatial hierarchies. By utilizing advanced methods, this methodology significantly outperforms existing methodologies, resulting in more reliable diagnostics in histopathological analysis.

The article is structured as follows: Section "Related works" presents the literature review, Section "The Proposed Model" outlines the proposed method, Section "Performance validation" details the results evaluation, and Section "Conclusion" concludes the study.

Related works

AlGhamdi11 presented the MN classification and segmentation employing the chaotic butterfly optimizer procedure with the DL (MNSC-CBOADL) method. The U-Net architecture was implemented for segmentation. Moreover, the Xception framework was used to make feature vectors. The deep belief network (DBN) model has been utilized for classification. The CBOA could be developed for the hyperparameter tuning process. Balasundaram et al.12 considered identifying and categorizing the structural features of the cytoplasm and nucleus parts of cancer cells. Automatic identification and classification have been performed with the help of the computerized analytical tool of the DL method. Residual blocks with small skips are utilized within the hidden layers of retained spatial data. A ResNet-based CNN could be used to execute end-to-end segmentation. Nuclei regions should be recognized through tubular structure morphology and colour features. In13, a 2-phase mitosis segmentation and classification technique called the SCMitosis was developed. The segmentation process with a higher recall rate was primarily accomplished via the introduced channel-spatial attention gate and depthwise separable convolution residual block. Besides, a classification model is cascaded to increase the effectiveness of identifying mitosis nuclei. Nemati et al.14 projected a hybridized technique to identify and categorize abnormal mitosis in breast HIs. This developed method includes 2 phases. In the first phase, DL approaches could be implemented to identify mitosis. Then, in the second phase, fuzzy-based techniques have been applied to classify mitosis. In15, an adapted automatic nuclei classification model for HIs is proposed. This technique utilizes the encoding–decoding architecture and leverages the segmentation sample. An innovative method was presented, including an adapted multi-kernel convolution (MKC) and multi-layer perceptron (MLP) model. The MLP model considers mining global contextual data of nuclei and micro-settings, and the MKC model regards removing local data over various accessible regions.

In16, an innovative Densely Connected Neural Network (DCNN) architecture was designed. The DCNN and Densely Connected Recurrent Convolutional Networks (DCRNs) frameworks have been implemented to process the nuclei classification. The R2U-Net and R2UNet-enabled regression algorithm, the UD-Net, is employed for segmenting the nuclei and corresponding tasks. In17, a novel cascaded-CNN UBCNN (cascaded CNN-based UNet) method including 3 measures was projected. Initially, an increased UNet +  + segmentation network was applied. Then, a sufficiently labelled cell nucleus dataset was transferred to an enhanced 2D-VNet network, and the cell nucleus was placed. Lastly, the attained cell image block was employed for training a CNN, and the candidate fixed region was screened to preserve the outcome of mitosis cells. Dumbhare et al.18 proposed a hybrid DL method that integrates deep-learned features acquired in the ResNet-50 architecture with hand-crafted features. This developed study employs the HoVer-Net as a baseline method introduced and adapted to combine hand-crafted features attained through 2 feature descriptors, namely histogram of oriented gradients (HOG) and local binary pattern (LBP). Goceri et al.19 propose a model in which nuclei segmentations are performed by employing an attention-aware adversarial network. Dense convolution layers and a hybrid attention module are also integrated into the adversarial network to enhance the performance of the segmentation. Alrowais et al.20 present an Enhanced Pelican Optimization Algorithm (EPOA) with a Deep Learning (DL) model for classifying mitotic and non-mitotic cells in breast histopathology images. The ShuffleNet technique is also employed for feature extraction, with hyperparameters tuned via the EPOA method, and an adaptive neuro-fuzzy inference system (ANFIS) is utilized for the classification and detection of MN. In21, vision transformer-based nuclei classification is proposed. Vision transformers can capture global features and improve the classifications’ performance.

Malibari et al.22 propose an artificial hummingbird algorithm (AHA) for MN classification. This technique utilizes PSPNet for segmentation, ResNet for feature extraction, and XGBoost for classification, with parameter tuning via the AHBA approach. Lijo and Janardhanan23 introduce a novel methodology for mitosis detection in HIs featuring a Bi-wolf optimization-based LP norm regularized deep CNN model. Delgado-Rodriguez et al.24 developed an automated tool to classify cell division in video sequences. A DL model is captured by employing video microscopy, cell division and training, achieving high classification accuracy. Gaire et al.25 present an automated model named csPWS-seg. Utilizing a U-Net model with an attention mechanism employs key structural and biological differences to improve segmentation accuracy. Anaam et al.26 introduce a deep active learning (DAL) model, which employs DL. Yao et al.27 introduce a point-supervised dense nuclei detection framework that employs morphology-based pseudo-labeling and position-based anchor optimization. The model also utilizes Position-based Anchor-quality estimation to filter out low-quality detections and implements an Adaptive Anchor Selector to optimize anchor selection. Anaam, Al-antari, and Gofuku28 present a DL framework incorporating a self-attention deep cross-residual network with an efficient GAN. It addresses the imbalance of mitotic and interphase cells utilizing the Info-WGANGP approach and data augmentation, resulting in the development of the Att-DCRNet model for classifying cell patterns in IIF HEp-2 medical images. Seyala and Abdullah29 aim to develop a robust clustering method using a nonparametric cubic B-spline model. Ali and Mohammed30 aim to systematically review and analyze existing research on AI methods.

The existing studies present various limitations in their methodologies. Incorporating multiple models may complicate training and enhance computational demands, affecting real-time applications. Sensitivity to image quality could impact performance, specifically with methods depending on residual blocks or intrinsic architectures, potentially resulting in false positives or overfitting in small datasets. Two-phase models introduce delays, while fuzzy approaches may yield ambiguous classifications. High computational needs for hyperparameter tuning could limit scalability, and the performance of vision transformers might rely heavily on extensive training datasets. Furthermore, the efficiency of the AHA is sensitive to parameter settings, and video quality variability could affect automated classification tools. These limitations underscore the threats of attaining reliable and effectual detection in various histopathological contexts. Despite enhancements in the DL model for MN classification, there still needs to be a gap in addressing the variability in image quality and the robustness of models across diverse datasets. Moreover, many existing methods need more real-time processing capabilities, limiting their practical application in clinical settings. Further exploration is required to improve model generalizability and streamline hyperparameter tuning to facilitate broad adoption in automated pathology.

The proposed model

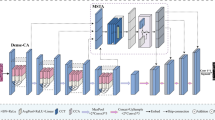
In this work, a COADL-MNSC methodology is proposed. The main objective of the COADL-MNSC methodology is to deploy the DL model for the segmentation and classification of MN. At the COADL-MNSC model, the diverse phases of processes include MF-based pre-processing, HAU-UNet-enabled segmentation, CapsNet-based feature extractor, COA-based hyperparameter tuning, and BiLSTM-based classification. Figure 1 shows the working process of the COADL-MNSC model.

Fig. 1
figure 1

Workflow of COADL-MNSC technique.

Full size image

Pre-processing

Initially, the COADL-MNSC technique utilizes MF for pre-processing. MF is essential in improving raw microscopic images for precise segmentation31. This model mitigates noise efficiently while conserving significant image details and edges. Unlike linear filtering methods, which can blur edges and delicate structures, MF replaces each pixel’s value with the median of neighbouring pixels, reducing the impact of outliers and impulsive noise. This characteristic is advantageous in applications with substantial image clarity for precise evaluation. Moreover, MF is computationally effective and straightforward, making it appropriate for real-time processing. By improving the quality of input images, MF crucially enhances the performance of subsequent techniques in the model, resulting in more reliable results in tasks such as segmentation and classification. Figure 2 illustrates the working flow of the MF model.

Fig. 2
figure 2

Workflow of the MF technique.

Full size image

MN images often show intrinsic noise, which interferes with accurate segmentation. MF changes all pixels with the median value of its neighbouring pixels, efficiently removing salt-and-pepper noise even while maintaining the different boundaries of nuclei. This denoising stage not only increases the visibility of MN but also supports the following image analysis, providing additional reliability and effective segmentation outcomes. The application of MF in the pre-processing pipeline is instrumental in formulating microscopy images for progressive analysis, enabling the identification and analysis of mitotic measures with increased accuracy.

Image segmentation

The COADL-MNSC technique uses the HAU-UNet model to segment the MN32. This model was chosen due to its advanced architecture, which integrates the merits of conventional U-Net with attention mechanisms. This incorporation allows the model to concentrate on relevant features while minimizing the impact of background noise, which is critical in biomedical image analysis. Its capability to handle varying sizes and shapes of nuclei enhances segmentation accuracy, particularly in intrinsic tissue samples. Moreover, the efficiency of the HAU-UNet model in training with limited annotated data makes it specifically appropriate for medical applications where labelled datasets are often scarce. Overall, this model presents a robust outcome for precise and reliable segmentation of MN, contributing to improved diagnostic insights in pathology.

The U‐Net architecture has become widely utilized in medical image segmentation. However, the decoder components might have problems recreating the complete data exactly. In downsampling, the loss of spatial data makes it complex for the decoder to recover accurate details, including contours and edges. This problem concerning tongue crack extraction is particularly prevalent. This problem differentiates crack edges at the coloured tongue body, which proved challenging33.

To overcome these challenges, the study presents the HAU‐net, which incorporates the \(\text{U}\)‐Net decoder into a Hybrid Parallel Attention Mechanism (HPAM). After the upsampling phase, three HPAM components have been integrated into the decoder network in \(U\)‐Net. Implementing multiple-track parallel attention models enables the synthesis of features in dissimilar scales during the encoder phase and feature extraction at the decoder phase.

The HPAM could not be embedded in the encoder since the downsampling of the U‐Net encoder results in data loss in the tongue crack images, leading to reduced detection accuracy. The HAU‐net model considers the applicable tongue crack data and feature maps of varying sizes by integrating the HPAM module during the decoder. Subsequently, this method efficiently improves the efficiency and accuracy of the model for identifying and detecting tongue cracks.

The process employed in the tongue crack extracting models includes two elements: Dice loss and cross‐entropy loss.

$${\mathcal{L}}_{total}={\mathcal{L}}_{BCE}+{\mathcal{L}}_{Dice}$$
(1)
$${\mathcal{L}}_{BCE}=-{\sum }_{i}\left({t}_{i}\text{ln}\left({\widehat{t}}_{i}\right)+\left(1-{t}_{i}\right)\text{ln}\left(1-{\widehat{t}}_{i}\right)\right)$$
(2)

Now, the cracked area of the tongue and cracked area of true values are \({t}_{i}\) and \({\widehat{t}}_{i}\), correspondingly. This study exploits the dice loss to handle the class imbalance problems:

$${\mathcal{L}}_{Dice}=1-\frac{2\cdot \langle {t}_{\left(h,w\right)},{\widehat{t}}_{\left(h,w\right)}\rangle +\sigma }{\| {t}_{\left(h,w\right)}|{|}_{1}+\| {\widehat{t}}_{\left(h,w\right)}{\| }_{1}+\sigma }$$
(3)

In Eq. (3), the pixel coordinate is denoted as \((h,w)\), and the Laplacian smoothing factor speeds up the convergence rate and is represented as \(\sigma\).

Loss functions significantly affect the performance of the proposed method. Although cross-entropy is commonly used and is nearly a default loss function, several works have indicated that hybrid loss functions in deep networks provide efficiency in segmentation and classification34.

CapsNet feature extractor

The CapsNet model is applied to the feature extraction process at this stage. The CapsNet has been mainly utilized to categorize handwritten numbers of the dataset of MNIST35. This model is chosen for its capability to preserve spatial hierarchies and relationships between features, which is significant for understanding intrinsic patterns in crowd data. Unlike conventional CNNs, CapsNet employs capsules to capture diverse properties of objects, allowing for an enhanced generalization across various viewpoints and occlusions. This capability improves crowd density estimation and anomaly detection robustness, specifically in challenging scenarios with overlapping individuals. Furthermore, CapsNet’s emphasis on dynamic routing between capsules facilitates more complex feature extraction, improving performance in detecting subtle discrepancies in crowd behaviour related to conventional models36. Overall, its innovative architecture gives substantial merit in efficiently analyzing crowd dynamics. Figure 3 shows the structure of the classical CapsNet model used in this work.

Fig. 3
figure 3

Structure of CapsNet model.

Full size image

In a classic CapsNet, six layers are generally accessible and mainly used to encode and decode. Although CNNs have been commonly used for feature extraction, they have limitations, such as losing spatial relationships of learned features. The advantages of CapsNets and their superiority over CNNs-based classification of medical images have been demonstrated in various works37. The convolutional layer is the first layer, monitored by a main layer containing one or many convolutional layers with a squashing process. Furthermore, it includes a label and digit capsule where dynamic routing arises. The latter three layers are FC layers employed in an image renovation.

The distinct convolutional layer stimulated the neurons using a dissimilar activation function. In contrast, the main caps layer used a non‐linear squashing process in Eq. (4) to renovate the neurons into a vector.

$${v}_{j}=\frac{||{S}_{j}|{|}^{2}}{1+||{S}_{j}|{|}^{2}}\frac{{S}_{j}}{||{S}_{j}||}$$
(4)

\({S}_{j}\) refers to the whole input to the capsule, and \({v}_{j}\) denotes the computerized output vector of the \(j\) capsule. The entire input to a capsule \({S}_{j}\) is considered in (6) over the biased sum in every prediction vector \({\widehat{P}}_{j|i}\) at the lowest layer capsule. The prediction vector is calculated using Eq. (5) to multiply the weight matrix \({W}_{ij}\) and output \({p}_{i}\) in the below layer.

$${\widehat{P}}_{j|i}={W}_{ij}{p}_{i}$$
(5)
$${S}_{j}={\sum }_{i}{k}_{ij}{\widehat{P}}_{j|i}$$
(6)

where \({k}_{ij}\) denotes the coupling constant calculated using Eq. (7) and dynamic routing (DR) procedures, DR is a procedure among the capsules to choose how to go through the system. It occurs with DR by contract among the highest and lowest capsules. The capsule at the highest level obtains an input at the lowest level capsule via contract repeatedly. It is suggested that only three iterations be employed due to the higher number of iterations that over-fit the method.

$${k}_{ij}=\frac{exp({n}_{ij})}{{\sum }_{k}exp({n}_{ik})}$$
(7)

where \({n}_{ij}\) signifies the \(\text{log}\) probability intended to utilize the softmax function, the amount of coupling constant \({k}_{ij}\) among capsule \(i\) and the highest layer must be 1. For computing the \({k}_{ij},\) \({n}_{ij}\) should be formulated by employing Eq. (8).

$${n}_{ij}\leftarrow {n}_{ij}+{\widehat{P}}_{j|i}\cdot {v}_{j}$$
(8)

The \({n}_{ij}\) value is \(0\), and by applying this, \({k}_{ij}\) and \({p}_{i}\) are obtained, which is an output of the preceding layer. By employing these 3 values, the subsequent range capsule input \({S}_{j}\) is computed.

For loss of margin, the loss has been computed in Eq. (9) for each category to define whether an exact object existed in the class.

$${M}_{l}={C}_{k}\text{max}(0, {u}^{+}-||{v}_{k}|{|}^{2})+\lambda (1-{C}_{k})\text{max}(0, ||{v}_{k}||-{u}^{-}{)}^{2}$$
(9)

where as \({C}_{k}=1\) if a digit of class \(k\) exists, \({u}^{-}=0.1\) and \({u}^{+}=0.9\) are the hyperparameters, which signifies the down loss weighting loss. An entire loss is the addition of the losses of complete digit capsules.

Hyperparameter tuning using COA

In this work, the hyperparameters are adjusted by utilizing the COA model38. This model presents a unique approach to hyperparameter tuning by replicating coatis’s adaptive foraging behaviour, allowing for efficient search space exploration. Its capability to balance exploration and exploitation assists in averting local optima, making it efficient in intrinsic parameter landscapes. COA portrays robust performance in optimizing multiple hyperparameters simultaneously, thereby mitigating computational time compared to conventional methods. Furthermore, its robustness across diverse datasets and model architectures improves its applicability in DL tasks, giving a competitive edge over other optimization techniques such as grid search or random search. This adaptability makes COA a valuable tool for fine-tuning model performance in diverse scenarios. Figure 4 represents the working flow of the COA technique.

Fig. 4
figure 4

Steps involved in the COA model.

Full size image

The CoatiOA has numerous stages, which are mentioned below:

  • Initialization stage: X is a matrix that holds the arbitrary early populace places as displayed in Eq. (10), where \(N\) denotes the coati’s number, and \(M\) specifies the problem size number. Every coati \(i\) place is exposed in Eq. (11). At the same time, \(r\) refers to an arbitrary variable among an interval range of (\(0\), 1), and \(l{b}_{j}\) and \(u{b}_{j}\) denote the lower and upper values of decision variable \(j\). The main role of all positions is measured, and a vector \(F\) with size \(NX1\) is made, as revealed in Eq. (12).

    $$X={\left[\begin{array}{l}{X}_{1}\\ \vdots \\ {X}_{i}\\ \vdots \\ {X}_{N}\end{array}\right]}_{N\times m}={\left[\begin{array}{lllll}{x}_{\text{1,1}}& \dots & {x}_{1,j}& \dots & {x}_{1,m}\\ \vdots & \ddots & \vdots & .& \vdots \\ {x}_{i,1}& \dots & {\chi }_{i,j}& \dots & {\chi }_{i,m}\\ \vdots & .& \vdots & \ddots & \vdots \\ {x}_{N,1}& \dots & {x}_{N,j}& \dots & {x}_{N,m}\end{array}\right]}_{N\times m}$$
    (10)
    $${X}_{i}: {x}_{i,j}=l{b}_{j}+r\cdot \left(u{b}_{j}-l{b}_{j}\right), i=\text{1,2},\dots ,N, j=\text{1,2},\dots ,m,$$
    (11)
    $$F={\left[\begin{array}{l}{F}_{1}\\ \vdots \\ {F}_{i}\\ \vdots \\ {F}_{N}\end{array}\right]}_{N\times 1}={\left[\begin{array}{l}F\left({X}_{1}\right)\\ \vdots \\ F\left({X}_{i}\right)\\ \vdots \\ F\left({X}_{N}\right)\end{array}\right]}_{N\times 1}$$
    (12)

  • Exploration Stage (Hunter search and Attack): The coatis should be separated into dual clusters in this stage. The primary cluster climbs a tree to panic the prey, and another cluster delays below a 3 to fall on the nervous prey. Coati can able to hunt the issue space carefully. The target of Coatis has been named Iguana. The location of the optimal member of the populace is indicated to be the location of the Iguana. The place of the 1st half of the coatis climbing the tree is represented in Eq. (13). While an Iguanas falls to the ground, its place could be randomized, affording to Eq. (14). The 2nd part of the coatis waits below three travels affording to Eq. (15).

    $$\begin{aligned} & X_{i}^{P1} :x_{i,j}^{P1} = x_{i,j} + r \cdot \left( {Iguana j - I \cdot x_{i,j} } \right), \\ & for i = 1,2, \ldots ,\frac{N}{2} and j = 1,2, \ldots ,m \\ \end{aligned}$$
    (13)
    $$Iguan{a}^{G} : Iguan{a}_{i}^{G}=l{b}_{j}+r\cdot \left(u{b}_{j}-l{b}_{j}\right),j=\text{1,2},\dots ,m,$$
    (14)
    $$\begin{aligned} & X_{i}^{P1} :x_{{{\text{i}},j}}^{P1} = \left\{ {\begin{array}{*{20}l} {x_{i,j} + r \cdot \left( {Iguana a_{j}^{G} - I \cdot x_{i,j} } \right),} \hfill & {F_{Iguana} < F_{i} ,} \hfill \\ {x_{i,j} + r \cdot \left( {x_{i,j} - Iguana_{j}^{G} } \right),} \hfill & {else} \hfill \\ \end{array} } \right. \\ & for i = \frac{N}{2} + 1,\frac{N}{2} + 2, \ldots ,N and j = 1,2, \ldots ,m \\ \end{aligned}$$
    (15)

    If the novel position \({X}_{i}^{P1}\) of \(i\) coati enhanced fitness value, the older place \({X}_{i}\) denotes retained utterly. But, not in the older location has kept affording to Eq. (16), whereas \({x}_{i,j}^{P1}\) denotes its \(j\) dimension, \({F}_{i}^{P1}\) signifies fitness value of novel place, \(r\) refers to real arbitrary number among (0 and 1), Iguana represents the place of the prey, \(Iguan{a}_{j}\) denotes its \(j\) dimension, \(I\) refer to integer either 1 or 2, \(Iguan{a}^{G}\) has the location of prey under the ground, \(Iguan{a}_{j}^{G}\) is its \(j\) dimension, \({F}_{lguan{a}^{G}}\) means the fitness value of position \(Iguan{a}^{G}\), and \(\lfloor \bullet \rfloor\) signifies the floor function.

    $$X_{i} = \left\{ {\begin{array}{*{20}l} {X_{i}^{P1} ,} \hfill & {F_{i}^{P1} < F_{i} } \hfill \\ {X_{i} ,} \hfill & {else} \hfill \\ \end{array} } \right.$$
    (16)

  • Exploitation stage (escaping from hunters): When a hunter assaults a coati, it travels to an arbitrary place toward its location in Eqs. (17) and (18). The novel place is a usual when it enhances the fitness values according to Eq. (19). The suffix \(P2\) specifies the place and fitness of coati at the 2nd stage, \(u{b}_{j}^{local} and l{b}_{j}^{local}\) denote the local upper and lower limits of the \(j\) decision variables, respectively.

    $$l{b}_{j}^{local}=\frac{l{b}_{j}}{t},u{b}_{j}^{local}=\frac{u{b}_{j}}{t}, where t=\text{1,2},\dots ,T$$
    (17)
    $$\begin{aligned} & X_{i}^{P2} :x_{i,j}^{P2} = x_{i,j} + \left( {1 - 2r} \right) \cdot \left( {lb_{j}^{local} + r \cdot \left( {ub_{j}^{local} - lb_{j}^{local} } \right)} \right) , \\ & i = 1,2, \ldots , N,j = 1,2, \ldots , m, \\ \end{aligned}$$
    (18)
    $$X_{i} = \left\{ {\begin{array}{*{20}l} {X_{i}^{P2} ,} \hfill & {F_{i}^{P2} < F_{i} } \hfill \\ {X_{i} ,} \hfill & {else} \hfill \\ \end{array} } \right.$$
    (19)

The COA model obtains a fitness function (FF) to achieve refined classification effectiveness. This designates an optimistic integer for signifying the greater act of the candidate’s decisions. The decrease in the classification error rate has been measured as FF, as shown by Eq. (20).

$$\begin{aligned} fitness\left( {x_{i} } \right) = & ClassifierErrorRate\left( {x_{i} } \right) \\ = & \frac{No. of\,misclassified\,instances}{{Total\,No. of\,instances}} \times 100 \\ \end{aligned}$$
(20)

Classification process

At last, the classification process is performed by implementing the BiLSTM model39. This technique is appropriate for classification tasks comprising sequential data because it can capture contextual data from past and future sequences. This bidirectional approach improves the model’s understanding of the temporal dependencies, allowing for more precise anticipations related to unidirectional models. BiLSTMs efficiently mitigate issues associated with vanishing gradients, making them robust for long sequences. Their architecture is adept at learning intrinsic patterns, which is advantageous for sentiment analysis or time-series classification tasks. Furthermore, incorporating attention mechanisms improves performance by allowing the model to concentrate on the most relevant parts of the input sequence. Overall, the merits of the BiLSTM technique in handling sequential data make it an ideal choice for classification applications. Figure 5 depicts the architecture of the BiLSTM model.

Fig. 5
figure 5

Structure of the BiLSTM approach.

Full size image

In the gradient architecture of RNN, once the time step is too large or too small, the gradient of RNN can quickly explode and disappear. As a result, LSTM exploits gating models for controlling information to resolve these problems and introduces input, forget, and output gates to remove certain content that is not significant to the present situation, thus extending the memory time of data and storing some prior data. The input gate of LSTM represents the hidden layer (HL) among the previous time step \({H}_{t-1}\) and the existing time step input \({X}_{t}.\) The fully connected layer evaluates the output.

$$Input gate:{I}_{t}=\sigma \left({X}_{t}{W}_{xi}+{H}_{t-1}{W}_{hi}+{b}_{i}\right)$$
(21)
$$Forget gate:{F}_{T}=\sigma \left({X}_{t}{W}_{xf}+{H}_{t-1}{W}_{hf}+{b}_{f}\right)$$
(22)
$$Gated unit: {\widetilde{C}}_{\text{t}}=\text{ tanh }\left({X}_{t}{W}_{xc}+{H}_{t-1}{W}_{hc}+{b}_{c}\right)$$
(23)
$${C}_{t}={F}_{r}\odot {C}_{r-1}+{I}_{r}\odot {\widetilde{C}}_{t}$$
(24)
$$Output gate: {\text{O}}_{t}=\sigma \left({X}_{t}{W}_{xo}+{H}_{t-1}{W}_{ho}+{b}_{o}\right)$$
(25)

where the smaller batch input of \(t\) he t time step is \({X}_{t},\) the amount of HLs is \(h\), \(\sigma\) is the sigmoid function, the HL of the previous time step is \({H}_{t-1}\), the offset input gate is \({b}_{i}\); weight matrices of input gates are \({W}_{xi}\) and \({W}_{hi}\), the candidate memory unit is \({\widetilde{C}}_{t}\), the weight matrix of gating units are \({W}_{xc}\) and \({W}_{hc}\), the weight matrices of forget gate are \({W}_{xf}\) and \({W}_{hf}\), the offset forget gate represents \({b}_{f}\); the offset term of gating unit is \({b}_{c}\), weight matrices of output gate are \({W}_{xo}\) and \({W}_{ho}\), the cell state at the existing and prior time are \({C}_{t}\), and \({C}_{t-1}\) as well as the offset output gate is \({b}_{o}\). \(\text{tan}h\) is the activation function whose values range within \([-\text{1,1}]\); the data flow in the HL is measured by increasing with \(\odot\) components\(.\) The output gate \({O}_{t}\) controls the data flow in the memory unit to the HL, and lastly, output \({H}_{\zeta }\) is represented as follows:

$${H}_{r}={\text{O}}_{t}\odot \text{tan}h\left({C}_{t}\right)$$
(26)

Unlike the LSTM, the BiLSTM model comprises forward and backward LSTM. The total data hidden in the information was considered while extracting data features from the reverse and forward directions. Later, the outcomes of two-method extraction were used at a particular method and summarized from 2D that could remove the effect of input information at a single LSTM under a last result to a specific range.

Performance validation

In this part, the performance validation of the COADL-MNSC technique is verified by employing an MN image dataset comprising 150 samples and two classes, as shown in Table 140. The suggested method is simulated using the Python 3.6.5 tool on a PC with an i5-8600k, 250GB SSD, GeForce 1050Ti 4GB, 16GB RAM, and 1TB HDD. The parameter settings are provided: learning rate: 0.01, activation: ReLU, epoch count: 50, dropout: 0.5, and batch size: 5.

Table 1 Details of the dataset.
Full size table

Figure 6 displays the confusion matrices attained by the COADL-MNSC approach below 60:40 and 70:30 of the training phase (TRPH)/testing phase (TSPH). The accomplished outcomes show the effectual detection of the mitosis and non-mitosis samples with all classes.

Fig. 6
figure 6

(a–b) confusion matrices of COADL-MNSC model under 60:40 of TRPH/TSPH and (c–d) 70:30 of TRPH/TSPH.

Full size image

The mitotic classification outcomes of the COADL-MNSC methodology with 60:40 of TRPH/TSPH are given in Table 2 and Fig. 7. The attained results denote that the COADL-MNSC technique proficiently detected the mitosis and non-mitosis samples. With 60% of TRPH, the COADL-MNSC technique gains an average \(acc{u}_{y}\) of 98.89%, \(pre{c}_{n}\) of 98.94%, \(rec{a}_{l}\) of 98.86%, \({F}_{score}\) of 98.89%, MCC of 97.80%, and \({G}_{measure}\) of 98.89%. Additionally, on 40% of TSPH, the COADL-MNSC method gets an average \(acc{u}_{y}\) of 96.67%, \(pre{c}_{n}\) of 96.77%, \(rec{a}_{l}\) of 96.77%, \({F}_{score}\) of 96.67%, MCC of 93.55%, and \({G}_{measure}\) of 96.72%, respectively.

Table 2 Mitotic classification analysis of the COADL-MNSC methodology under 60:40 of TRPH/TSPH.
Full size table
Fig. 7
figure 7

Average outcome of the COADL-MNSC approach with 60:40 of TRPH/TSPH.

Full size image

The \(acc{u}_{y}\) curves for training (TR) and validation (VL) demonstrated in Fig. 8 for the COADL-MNSC under 60:40 of TRPH/TSPH provides valued insights into its analysis with multiple epochs. Predominantly, it has made continuous progress in both TR and TS \(acc{u}_{y}\) with increased epochs, displaying the model’s capabilities in learning and finding patterns in data of the TR and TS. The upward trend in TS \(acc{u}_{y}\) highlights the model’s adaptability to the TR dataset as well as the capacity to produce exact predictions on unobserved data, emphasizing superior generalization proficiencies.

Fig. 8
figure 8

\(Acc{u}_{y}\) curve of the COADL-MNSC approach with 60:40 of TRPH/TSPH.

Full size image

Figure 9 illustrates an extensive overview of the TR and TS loss values for the COADL-MNSC methodology with 60:40 of TRPH/TSPH in diverse epochs. This TR loss dependably minimizes as the model raises its weights to lessen classification errors in two datasets. The loss curves signify the model’s alignment with the TR database, emphasizing its ability to capture patterns competently in these datasets. Noteworthy is the continuous upgrading of parameters in the COADL-MNSC approach, which targets reducing discrepancies among predictions and actual TR labels.

Fig. 9
figure 9

Loss curve of the COADL-MNSC model on 60:40 of TRPH/TSPH.

Full size image

Regarding the PR curve described in Fig. 10, the findings affirm that the COADL-MNSC technique on 60:40 of TRPH/TSPH constantly accomplishes enriched PR values at each class. These findings underscore the model’s efficient capacity for discriminating among several classes, highlighting its effectiveness in accurately recognizing class labels.

Fig. 10
figure 10

PR curve of the COADL-MNSC technique under 60:40 of TRPH/TSPH.

Full size image

In addition, in Fig. 11, the ROC curves created by the COADL-MNSC model are exhibited at 60:40 TRPH/TSPH, signifying its proficiency in distinguishing amongst classes. These curves offer valuable insights into how the TPR and FPR trade-offs differ at dissimilar classification epochs and thresholds. The obtained results emphasize the model’s accurate classification efficiency on different class labels, underscoring its effectiveness in addressing diverse classification challenges.

Fig. 11
figure 11

ROC curve of the COADL-MNSC methodology at 60:40 of TRPH/TSPH.

Full size image

The mitotic classification analysis of the COADL-MNSC methodology under 70:30 of TRPH/TSPH is defined in Table 3 and Fig. 12. The accomplished findings represent the COADL-MNSC method proficiently recognized the mitosis and non-mitosis samples. According to 70% of TRPH, the COADL-MNSC technique achieves an average \(acc{u}_{y}\) of 95.21%, \(pre{c}_{n}\) of 95.41%, \(rec{a}_{l}\) of 95.21%, \({F}_{score}\) of 95.23%, MCC of 90.62%, and \({G}_{measure}\) of 95.27%. Besides, with 30% of TSPH, the COADL-MNSC technique acquires an average \(acc{u}_{y}\) of 97.83%, \(pre{c}_{n}\) of 97.83%, \(rec{a}_{l}\) of 97.83%, \({F}_{score}\) of 97.78%, MCC of 95.65%, and \({G}_{measure}\) of 97.80%, correspondingly.

Table 3 Mitotic classification analysis of the COADL-MNSC technique on 70:30 of TRPH/TSPH.
Full size table
Fig. 12
figure 12

Average outcome of the COADL-MNSC model with 70:30 of TRPH/TSPH.

Full size image

The \(acc{u}_{y}\) curves for training (TR) and validation (VL) represented in Fig. 13 for the COADL-MNSC technique with 70:30 of TRPH/TSPH gives valued insights into its analysis with numerous epochs. Primarily, it has a continual development in both TR and TS \(acc{u}_{y}\) with better epochs, which showcases the model’s capabilities to learn and find patterns in data of the TR and TS. The upward tendency in TS \(acc{u}_{y}\) highlights the model’s versatility to the TR dataset and its capacity to create precise predictions on unnoticed data, emphasizing higher generalization proficiencies.

Fig. 13
figure 13

\(Acc{u}_{y}\) curve of the COADL-MNSC method under 70:30 of TRPH/TSPH.

Full size image

Figure 14 shows a wide-ranging overview of the TR and TS loss values for the COADL-MNSC approach with 70:30 of TRPH/TSPH in varied epochs. This TR loss consistently diminishes as the model increases its weights for declining classification errors at two datasets. The loss curves indicate the model’s alignment with the TR database, underscoring its ability to capture patterns in these datasets adeptly. Noteworthy is an incessant upgrading of parameters in the COADL-MNSC method, which aims to decrease discrepancies among predictions and actual TR labels.

Fig. 14
figure 14

Loss curve of the COADL-MNSC model with 70:30 of TRPH/TSPH.

Full size image

The PR analysis represented in Fig. 15 exhibited that the COADL-MNSC technique under 70:30 of TRPH/TSPH persistently achieves improved PR values in every class. These accomplished findings underscore the efficient capacity of the model for discriminating among numerous classes, highlighting its effectiveness in precisely recognizing class labels.

Fig. 15
figure 15

PR curve of the COADL-MNSC technique under 70:30 of TRPH/TSPH.

Full size image

Furthermore, in Fig. 16, the ROC curves produced by the COADL-MNSC model are presented at 70:30 TRPH/TSPH, indicating its proficiency in differentiating amongst classes. These curves give valued insights into how the trade-off between TPR and FPR differs at diverse classification epochs and thresholds. The acquired results emphasize the model’s accurate classification adeptness on various class labels, underscoring its effectiveness in addressing diverse classification challenges.

Fig. 16
figure 16

ROC curve of the COADL-MNSC technique on 70:30 of TRPH/TSPH.

Full size image

The comparison analysis of the COADL-MNSC approach with recent models is provided in Table 4 and Fig. 17. The results specify that the DHE-Mit and DenseNet201 models obtain worse performance. Along with that, the Xception-BOA-DBN, Xception-DBN, and AHBATL-MNC models attain slightly boosted results. Although the MNSC-CBOADL technique accomplishes reasonable performance, the COADL-MNSC technique exhibits superior results with a maximum \(acc{u}_{y}\) of 98.89%, \(pre{c}_{n}\) of 98.94%, \(rec{a}_{l}\) of 98.86%, and \({F}_{score}\) of 98.89%. Thus, the COADL-MNSC technique is applied to enhance classification results.

Table 4 Comparison analysis of the COADL-MNSC technique with other models11.
Full size table
Fig. 17
figure 17

Comparison analysis of the COADL-MNSC technique with other models.

Full size image

Table 5 and Fig. 18 illustrates the computational time (CT) analysis of the COADL-MNSC approach with recent methods. The methods and their corresponding CTs in seconds are as follows: COADL-MNSC attained a time of 7.66 s, while MNSC-CBOADL model took 14.89 s. The Xception-BOA-DBN method recorded a time of 14.80 s, and the Xception-DBN approach took 13.29 s. AHBATL-MNC completed its process in 10.37 s, followed by DHE-Mit at 12.64 s, and DenseNet-201, which needed 14.43 s.

Table 5 CT analysis of the COADL-MNSC technique with existing methods.
Full size table
Fig. 18
figure 18

CT analysis of the COADL-MNSC technique with existing methods.

Full size image

Conclusion

In this manuscript, the COADL-MNSC technique is proposed. The main objective of the COADL-MNSC method is to deploy the DL approach for the segmentation and classification of MN. In the COADL-MNSC method, the diverse phases of processes include MF-based pre-processing, HAU-UNet-based segmentation, CapsNet-based feature extractor, COA-based hyperparameter tuning, and BiLSTM-based classification. Primarily, the COADL-MNSC technique utilizes MF for pre-processing. Besides, the COADL-MNSC technique uses the HAU-UNet model to segment the MN. Moreover, CapsNet is implemented for the feature extraction method, and hyperparameters are adjusted by employing the COA model. Lastly, the classification process is performed by using the BiLSTM model. Extensive simulations are performed under the MN image dataset to exhibit the excellent performance of the COADL-MNSC methodology. The experimental validation of the COADL-MNSC methodology portrayed a superior accuracy value of 98.89% over existing techniques under diverse measures. As is known, deep neural networks need large datasets. Different augmentation algorithms have been employed to address various problems caused by deep networks and to enhance the generalization ability, reliability, and robustness of the methods. Therefore, the COADL-MNSC technique can be tested with the increased data as an extension of this work. Additionally, an intensity normalization was applied using the COADL-MNSC technique. Intensity inhomogeneity is an important issue affecting the methods’ performance, and various normalization approaches are applied to medical images. As a future work, an effective intensity normalization step can be integrated into the pre-processing stage to enhance the performance of the COADL-MNSC technique. Future work should explore incorporating multi-modal imaging data to improve the robustness of MN segmentation. Furthermore, developing adaptive algorithms that dynamically adjust to varying tissue types and conditions could improve accuracy. Finally, integrating user feedback mechanisms could refine model anticipations and assist real-time clinical applications.