A recursive embedding and clustering technique for unraveling asymptomatic kidney disease using laboratory data and machine learning

Abstract

Traditional methods for diagnosing chronic kidney disease (CKD) via laboratory data may not be capable of identifying early kidney disease. Kidney biopsy is unsuitable for regular screening, and imaging tests are costly and time-consuming. Several studies have implemented artificial intelligence (AI) to detect CKD. However, these studies used small datasets, had overfitting problems, lacked generalizability, or used complex algorithms that may require additional computational resources. In this study, we collected and analyzed center-based data and used a recursive embedding and clustering technique to reduce their dimensionality. We identified three clusters from 1600 records. We focused on the second cluster, as most of the characteristics had values in the normal ranges. Normal range values for most indicators generally represent stable kidney function with minor signs of strain, which often remain asymptomatic. Creatinine and eGFR levels within the threshold ranges indicate early kidney stress without filtration issues, which require close monitoring. The gradient-boosting algorithm showed superior performance among all algorithms in detecting these clusters. We evaluated an additional 400 unlabeled records to validate our method. This research can help clinicians automatically detect initial signs in numerous patients via routine tests to prevent the consequences of late-stage CKD detection.

Introduction

The kidney is an important organ in the body, responsible for maintaining chemical balance by eliminating waste and surplus water from the blood and keeping certain elements, including sodium, potassium, and calcium, at normal levels. Chronic kidney disease (CKD) is a long-term condition that predisposes the individual to end-stage renal disease, premature death, and cardiovascular diseases^1,2. Understanding the risk factors and prevalence of CKD is critical, and identification of its earlier stages is needed to develop suitable prevention strategies³. People at any age can develop kidney disease, but some are more likely to have it than others if they present with risk factors associated with this condition, including sex, family history, obstructive sleep apnea, hypertension, diabetes, smoking, peptic ulcer disease, history of acute kidney disease, and hyperlipidemia^4,5,6,7,8.

Screening and diagnosing CKD⁹ involves measuring serum creatinine levels, using a serum creatinine-based equation, assessing the urine albumin/creatinine ratio, and estimating the glomerular filtration rate (eGFR)^10,11 along with performing urinalysis¹². Urine and blood tests are two laboratory tests that can be used to detect kidney diseases^13,14,15,16. Most patients with early kidney disease are asymptomatic; in these cases, urine tests are used to detect protein in the urine, a condition called “albuminuria”, whereas blood tests are used to determine the creatinine level, which is used to calculate the GFR. There are five important stages prior to kidney failure; kidney damage, characterized by albuminuria and a normal GFR, followed by a stage characterized by a mild decrease in the eGFR, then a moderate decrease and then a severe reduction in the GFR and subsequent kidney failure¹⁷.

Identification and screening of CKD in its earlier stages is critical^18,19,20. Among the tools currently employed for these tasks, artificial intelligence (AI)^21,22,23 has emerged as an important group of methods for identifying the early signs of CKD²⁴, providing personalized treatment plans and optimizing CKD management^25,26. AI has been applied to various medical imaging modalities, such as magnetic resonance imaging (MRI)²⁷, ultrasound (US)^28,29,30, computed tomography (CT)³¹, and retinal imaging^32,33, to identify micropathological changes and diagnose renal fibrosis³⁴. AI has even been used to detect CKD from electrocardiogram (ECG) data³⁵. Machine learning (ML) techniques have been used in several studies^28,36 along with explainable AI in the management of CKD patients, chiefly using SHapley Additive explanations (SHAP) and partial dependency plots (PDPs). We utilized PDP as a visualizing tool in ML to understand the connection between features and the prediction of a model. They help with the interpretation of complex models, like gradient boosting in our research.

Additionally, ML algorithms have been used for the early detection of kidney disease with high accuracy³⁷. The authors of a previous study³⁸ introduced a novel enhanced hybrid mud ring network (EHMRN) that uses data generated from generative adversarial networks (GANs) to validate their model for the early detection of CKD. In their study, Apache Spark was employed for security and privacy concerns. Various ML algorithms³⁹ have also been used to detect CKD via principal component analysis (PCA). A real-time web application based on an ML model was developed to assist in diagnosing CKD and prevent complications such as hypertension, anemia, and renal failure⁴⁰. Several feature section techniques were applied, and validation approaches were used to enhance the performance of the model.

Interoperability is critical in AI models. ML models have been developed to predict CKD, and explainable AI-based strategies allow clinicians to understand the rationale underlying the prediction⁴¹. ML techniques have been used to predict CKD and classify its different stages⁴² through both binary and multiclass classification. Table 1 shows a comparison between our study and other studies in the literature.

Table 1 Comparative analysis between our study and other studies in the literature.

The primary novel idea of the present research is to leverage advanced embedding and clustering techniques—specifically recursive t-distributed stochastic neighbor embedding (t-SNE) and k-means clustering—to analyze laboratory data related to CKD. By identifying new correlations and enabling the use of ML to automate the identification of CKD in its earlier stages, this research aims to uncover critical insights that could improve patient management and outcomes and support explainability. The objectives of this study are as follows:

• Analyze various significant features of CKD using laboratory data to identify early signs and avoid later diagnosis and complications.

• Apply recursive t-SNE to reduce the dimensionality of the dataset, facilitating visualization and helping to identify inherent structures within the data.

• Use k-means clustering to categorize the data into distinct groups based on similarities in laboratory parameters.

• Analyze the clusters to uncover new correlations between laboratory parameters that may indicate relationships with CKD.

• On the basis of the identified clusters and correlations, implement an automated ML models to detect individuals with early indicators of CKD.

• Create a ML model to label new data based on the insights gained from clustering and correlation analysis.

In this study, we had to cluster the dataset because it did not have any labels. After clustering, it should be possible to compare the resulting clusters. Our null hypothesis is that there are no significant differences among the clusters in our dataset. We employed several statistical tests to assess this hypothesis, and then we employed ML models to detect clusters.

This paper is arranged as follows. The next section presents the methodology. Afterward, we present our results and discussion section. Finally, the conclusions of the study are presented.

Methods

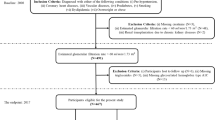
We used a two-step collection method to make sure that the trained ML model is validated on a separate dataset to ensure that our model is generalized and robust. Figure 1 shows the overall method where we applied both unsupervised learning through clustering and supervised learning through ML algorithms to automate the cluster’s classification process.

Data collection

We aim to gather high-quality and generalizable data from various populations. Our dataset was collected from the Al-Borg Laboratory Center consisting of 2000 records with 18 features. The study protocol was approved by Al-Borg Laboratory Center {IRB approval number: (No08/23} and was carried out in accordance with relevant guidelines and the Helsinki Declaration. Patient consent was waived off due to retrospective nature of the study based on the request of the research team. Data collected were anonymized prior to exporting into an excel sheet. We specifically collected 1600 records based on predefined inclusion and exclusion criteria. We used this dataset for unsupervised clustering and for training a supervised ML model to predict clusters. Then, we obtained another set of 400 records to test the model’s applicability with new unseen data. These records have some missing values to make them more like real-world situations. We did not use these 400 samples for training or clustering. Instead, they were used as a validation set that had never been seen before to see how well the model could find and predict cluster assignments in data that had never been seen before. The total of these 2000 cases represents the entire dataset available for analysis in this study.

Based on several studies^43,44, we selected 2000 records because they can be effective and sufficient for detecting early signs of CKD and represent a large population. We concentrated on routine lab tests and 18 significant CKD-related variables, as previous studies have highlighted the importance of these real-world demographic and laboratory test variables, such as creatinine in serum, and eGFR, in predicting CKD and based on clinicians involved (domain knowledge). We collect data under the following criteria:

The inclusion criteria include individuals of all ages who undergo routine laboratory tests. At the time of data collection, complete data for at least 60% of the 18 laboratory features crucial for CKD detection at early stages was available, and there was no sign of end-stage renal disease (ESRD) or acute kidney injury (AKI).

For exclusion criteria, we exclude all records with more than 40% missing data for critical features, patients with conditions known to affect kidney function (e.g., severe infections, chronic inflammatory diseases, and pregnancy) that might confound CKD indicators, and individuals with incomplete data for essential features related to CKD detection.

Table 2 lists these features, which are related mainly to kidney diseases and signs of infection, such as absolute eosinophil counts and absolute eosinophil counts, along with their descriptions.

Table 2 Description of features in the dataset.

Data preprocessing and analysis

Patient identifiers were removed to protect privacy; any duplicates were removed, and any record with missing data above 40% or missing for essential features was excluded according to the exclusion criteria. Values missing from at most 40% of the records were imputed for BMI. For this numerical feature, we imputed the values using the means. All the data were quantitative except for sex, which was categorical, for which males are represented as 1 and females as 0 with no missing values.

We applied a T-test to compare the BMI feature imputed using different methods (mean vs. KNN and mean vs. MICE). The T-statistics were close to zero (− 0.0044 and − 0.0043), and the P-values were high (0.9965 and 0.9966) consequently, which means that there were no statistically significant differences in the BMI means between the methods. These findings in Fig. 2 indicates that the chosen imputation method has no impact on the overall mean BMI values in our dataset. Therefore, all three imputation methods give comparable results for BMI imputation.

We normalized all the features to range between 0 and 1 via the min–max scaling method to ensure that all the features contributed equally to the K-means clustering by applying the following equation:

$$x^{\prime}=~\frac{{{x_i} - Min~\left( x \right)}}{{\hbox{max} \left( x \right) - Min\left( x \right)}}$$

(1)

Here, x′ is the normalized value of x_i, min(x) is the minimum value of the feature, and max(x) is the maximum value of the feature in the dataset. Table 2 shows the mean, standard deviation, and variance of the features in the dataset.

We used both pre-selected features based on clinical relevance (domain knowledge) and Spearman correlation^45,46 to assess the relationships between these features. to make sure the ones we picked are both statistically valid and clinically meaningful. This method aligns with best practices in predictive modeling and medical research.

These tests collectively provide insight into kidney function and systemic health, facilitating accurate diagnosis and management of CKD and its complications.

Recursive embedding and clustering technique

A recursive embedding and clustering (REC) is a method that aims to increase the interpretability and explainability of the clustering results. It involves an iterative process of embedding data into lower-dimensional spaces and applying clustering algorithms, with a focus on retaining the structure of the original data while making the results interpretable^47,48,49. We adjusted the PCA, which is primarily used for dimensionality reduction and noise filtering, during this step, enhancing the efficiency and effectiveness of the clustering algorithms.

• 1. Embedding Data: We used t-SNE on the dataset^50,51,52 to create lower-dimensional embeddings. This algorithm assesses complex and nonlinear patterns and preserves local relationships between data points. t-SNE follows several steps involving probability distributions that focus on similarities between data points in high dimensions. These include the conditional probability and symmetric probability.

Conditional Probability (${p_{ij}}$): This measures how likely data point j is a neighbor of data point i, given that they are represented as high-dimensional data. The formula uses the Gaussian kernel as follows:

$${p_{ij}}=~\frac{{\exp \left( { - ~\frac{{{x_{i~}} - ~{x_j}^{2}}}{{2~\sigma _{i}^{2}}}} \right)}}{{\mathop \sum \nolimits_{{k \ne i}} \exp \left( { - ~\frac{{{x_{i~}} - ~{x_k}^{2}}}{{2~\sigma _{i}^{2}}}} \right)}}$$

(2)

where:

${x_{i~}}and~{x_{j~~}}$ are the high-dimensional vectors for data points i and j. ${\sigma ^2}~$ is a parameter that controls the width of the neighborhood. ${x_{i~}} - ~{x_j}~$ is the Euclidean distance between points i and j.

Symmetric Probability (${p_{ij}}$): To make the distribution symmetric (meaning that the probability of i being a neighbor of j is the same as that of j being a neighbor of i), where N is the total number of data points. We average the conditional probabilities:

$${p_{ij~=~\frac{{\left( {{p_{ij}}+~{p_{ji}}} \right)}}{{2 \times ~N}}}}$$

(3)

Then, we studied the probability distributions, which focus on similarities between data points in low dimensions. Here, we focused solely on the conditional probability.

Conditional Probability (${q_{ij}}$): This mirrors ${p_{ij}}$ but for low-dimensional embedding (using the same Gaussian kernel but with low-dimensional coordinates).

$${q_{ij}}=~\frac{{\exp \left( { - ~\frac{{{y_{i~}} - ~{y_j}^{2}}}{2}} \right)}}{{\mathop \sum \nolimits_{{k \ne i}} \exp \left( { - ~\frac{{{y_{i~}} - ~{y_k}^{2}}}{2}} \right)}}$$

(4)

where ${y_{i~}}$ and ${y_{j~}}$ are the low-dimensional coordinates of points i and j.

The cost function for t-SNE is the Kullback‒Leibler (KL) divergence, which measures how different the probability distributions p and q are. The main objective of t-SNE is to minimize the following function:

$$C={D_{kl~~}}\left( {P\parallel Q} \right)=~\mathop \sum \limits_{{i,j}} {p_{ij~~}}\log \left( {\frac{{{p_{ij}}}}{{{q_{ij}}}}} \right)$$

(5)

Afterward, we applied an optimization technique named gradient descent to minimize the KL divergence and find the low-dimensional coordinates (${y_{i~}}$) that best represent the high-dimensional data.

Perplexity is a tuning parameter in t-SNE that helps control the balance between local and global data relationships during the clustering process.

• 2. Clustering: Clustering aims to group similar data points together, revealing hidden patterns and structures that might not be immediately obvious on initial analysis. We applied K-means to the embedded data with the goal of finding cluster assignments that minimize the sum of squared errors (SSE). We can write this mathematically as:

$$SSE=~\mathop \sum \limits_{{i=1}}^{n} {x_{i~}} - {c_{{j_i}}}^{2}$$

(6)

where:

n is the number of data points. ${x_{i~}}$ is the $ith$ data point. ${c_{{j_i}}}$ is the centroid of the cluster to which data point i is assigned. ${x_{i~}} - {c_{{j_i}}}^{2}$ is the squared Euclidean distance between data point i and its assigned cluster centroid.

In other words, the goal is to find cluster assignments that make the overall distance (squared) between each data point and the cluster centroid as small as possible by minimizing the SSE formula. We interpreted the results of k-means clustering through silhouette scores, which indicate the quality of the clustering. Evaluating the performance of a model is critical to understanding its effectiveness and reliability. To do this, we calculated the accuracy, precision, recall, and the F1 score, plotted the receiver operating characteristic (ROC) curve (and obtained the corresponding area under the curve (AUC)), and generated a confusion matrix.

Results and discussion

Table 3 shows the 40 most correlated features from the collected dataset. Age_Years feature shows a typical age distribution in the sample population. The platelet counts suggested normal platelet levels. Total protein in serum shows a shift in the distribution that might indicate protein loss. The creatinine value shows creatinine levels, a direct indicator of kidney function, and a peak in a higher range could indicate the presence of CKD. The distribution of absolute eosinophil count shows a narrow peak, suggesting few fluctuations in eosinophil levels among the subjects. Higher absolute basophil counts can be observed in chronic inflammation. A low peak in the absolute lymphocyte count might indicate immune suppression. High BMI values are associated with increased CKD risk. A shift to higher values in the BUN distribution might indicate kidney function impairment. A high total leucocyte count suggests infection or inflammation. The eGFR is a key marker for CKD, with lower values indicating reduced kidney function. A peak at a low eGFR could signify the presence of advanced CKD. Low sodium levels could indicate fluid imbalances often observed in CKD patients. Elevated potassium levels in CKD can lead to complications such as hyperkalemia, which is associated with severe health risks. Low calcium levels are common in CKD-related bone disease. High values of the BUN/creatinine ratio may indicate reduced kidney function. Low albumin is associated with malnutrition and advanced CKD. There are no distinct clusters for any feature and there are many overlaps between different data points.

Table 3 Correlations between features.

Principal component analysis (PCA)

We focused on the following features to understand the results of PCA⁵³: collect_year, age_years, BMI, sex, creatinine in serum, eGFR, BUN, total protein in serum, albumin in serum, sodium (Na) in serum, potassium (K) in serum, calcium in serum (Total), the BUN/creatinine ratio, platelet count, absolute eosinophil count, and absolute lymphocyte count. The explained variance (95%) is the proportion of the dataset’s total variance that is explained by the principal components.

These selected components together explain 95% of the variance, suggesting that a relatively small number of components can effectively summarize the data.

We obtained a cumulative variance of 0.954, which means that the first few principal components together explain 95.4% of the total variance in the dataset. This is generally a good amount of explained variance, suggesting that the selected components capture most of the information in the data. The component variance (0.29) indicates that the variance explained by the individual component is 0.29, or 29%. This suggests that this particular component explains a significant portion of the variance on its own.

We adjusted the global structure of the features as the first step, obtaining the first embedding through t-SNE. We got the results of six clustering processes via k-means following the acquisition of six embeddings via t-SNE which each yielded 3 clusters with cosine and Manhattan distance metrics. Clustering and measuring distance metrics are essential for grouping similar data together after we excluded outliers from the dataset. By grouping similar records, we reduce the overall number of records until, after the sixth iteration of clustering, the silhouette score stabilized for 3 clusters with 0.410 to 0.412 scores. We are using K-means clustering, which is sensitive to outliers, and we applied a distance-based method to remove points that were very far from the centroid. This is because these outliers can introduce noise and lead to overfitting.

The optimization was initialized with KMeans++, 10 reruns limited to 100 steps for 1545 instances after removing outliers and focusing on the top features, including collect_year, sex_name, age_years, BMI, Platelet count, Blood urea nitrogen (BUN), Total protein in serum, Estimated glomerular filtration rate (eGFR), BUN/Creatinine Ratio, Calcium in serum (total), Potassium (K) in serum, Albumin in serum, Creatinine in serum, and Sodium (Na) in serum.

Table 4 shows that the dataset decreased to 1581 after a first cosine distance clustering process. Metric-specific requirements likely resulted in the removal of 19 records; records with zero vectors or near-zero variance are excluded, as they have no significance for angular similarity. Subsequent rounds using the Manhattan distance decreased the dataset to 1566,1561, and eventually 1551, due to outlier and noise reduction. At this stage, the silhouette score increased slightly from 0.410 to 0.411, suggesting that the eliminated records may have added noise or ambiguity to the clusters. The 1566 records created a more stable and improved dataset for subsequent rounds. This stage most likely set the basis for increased clustering quality in the following phases. The Manhattan distance, which is sensitive to magnitude variations, likely identified extreme values or undefined records as outliers during repeated clustering. We used the cosine distance metric in the final stage. This created a stable dataset of 1545 records that didn’t decrease any further in the fifth or sixth rounds of clustering. The number of clusters remained at three throughout the whole process.

Table 4 Similar grouped data for six times of clustering.

The silhouette score increased marginally, from 0.410 in the first step to 0.412 at the end of the process, showing some improvement in cluster quality. The score’s stability and the constant number of clusters give strong indication that the clustering method efficiently refined the dataset without changing the clusters’ basic structure.

Figure 3a shows the scatter plots and box plots of the data for each of the three clusters. Cluster 1 (C1) had the lowest number of records, whereas cluster 2 (C2) had the greatest number of data records, followed by cluster 3 (C3), which had a similar size but fewer data records.

It is obvious that the clusters are highly separated from the second round of clustering. Cluster C1 contains 187 records, cluster C3 contains 614 records, and cluster C2 contains 765 records. With a total of 1545 records at the sixth round, a chi-square statistic of 3132, 4 degrees of freedom, and a p value of 0, we have strong evidence to reject the null hypothesis and conclude that there are significant differences among the groups in the dataset.

Figure 3b shows the scatter plot for the validation dataset after prediction. The ANOVA value of 2857 suggests the presence of significant differences among the means of the three clusters.

The clustering revealed several patient groups with a range of important demographic and laboratory features in Fig. 3c. These groups provide clinically significant new perspectives on early asymptomatic CKD diagnoses. We found that C1 represents the general healthy population or with normal lab values doing routine tests. C2 consists of individuals who show unremarkable renal problems in a few features, although they are asymptomatic. C3 comprises individuals who likely have early kidney disease symptoms but do not exhibit signs of ESRD or AKI.

Cluster analysis

We employed sieve diagrams in Fig. 4 to understand the cluster characteristics. Figure 4 shows the distribution of data points across a 3 × 3 grid of clusters, labeled C1, C2, and C3.

The color coding indicates the density or concentrate on of data points within each cluster, with red representing higher density and blue representing lower density. The legend on the left provides the cluster number and the total number of data points (N = 1545). The chi-square statistic (χ2 = 3090.00) and the associated p value (p = 0.000) suggest that the distribution of data points across the clusters is statistically significant. The size of each tile represents the number of data points (or density) in that particular range. Larger areas indicate more data points for that category, whereas smaller areas indicate fewer data points. This image shows that the dataset can be divided into three distinct groups on the basis of patterns in the sodium and potassium data.

The clusters provided can be used to interpret CKD on the basis of the variation in kidney-related biochemical markers (e.g., creatinine, blood urea nitrogen, and eGFR) and other associated parameters, such as electrolytes, proteins, and immune counts. Below is a cluster-based interpretation for CKD.

According to these values, indicators for the early stages of CKD in asymptomatic individuals on the basis of laboratory data and demographic trends include the following:

Collect_year is from 2017 to 2022. Age 40 to 52 years represent middle-aged individuals at potential risk for CKD may show slight reductions in kidney function without obvious symptoms. This group may have mild eGFR decline or slight creatinine elevation, indicating a risk of early-stage disease.

An equal distribution may indicate no sex-based risk. BMI between 24.20 kg/m² and 31.25 kg/m² where overweight or mild obesity is linked to increased risk for developing CKD. This is often a reversible risk factor if lifestyle changes can be implemented before symptoms appear. Absolute eosinophil count between 0.180 and 0.250 × 10⁹ cells/L is indicating normal immune function, but any slight increases may be observed in response to allergies or minor infections, which may indirectly affect kidney function. Absolute lymphocyte count between 1.92 and 2.44 × 10⁹ cells/L is indicating a balanced immune response, which is crucial for avoiding infections that worsen kidney health. Absolute basophil count: Mid-range counts between 0.02 and 0.03 × 10⁹ cells/L reflect balanced immune health with no evident inflammation. Total leucocytic count: Counts between 5.09 and 6.50 × 10⁹ cells/L indicate the normal range and no active infection; any minor elevations within this range might suggest early immune responses. Creatinine in serum: 0.80–0.88 mg/dL is within normal range, but it requires additional monitoring as it is close to the upper range limit of 1.2 mg/dL. eGFR: 60–65 mL/min/1.73 m² indicates early CKD patients with mild functional decline, generally asymptomatic but requiring monitoring to prevent further progression. Blood urea nitrogen (BUN) with 1 to 4 mg/dL indicates normal range, suggesting efficient kidney function without signs of advanced dysfunction. Total protein in Serum: 7.2–7.3 g/dL is within normal range and no evident protein loss, reflecting good nutritional status. Albumin in serum: 4.3–4.4 g/dL provides normal levels, indicative of adequate nutritional status and minor to no proteinuria. Sodium (Na) in serum: 139 to 140 mEq/L indicates normal sodium levels which provides proper fluid balance. Potassium (K) in serum: 4.4 to 4.5 mEq/L indicates normal healthy balance. Calcium in serum: 7 to 9 mg/dL provides normal calcium levels without signs of bone metabolism issues. BUN/creatinine ratio: 16.2–18.9 indicates normal balanced filtration and normal kidney function. Platelet count: 233 to 315 × 10⁹ cells/L indicates normal adequate platelet levels without bleeding risk and good bone marrow health.

While other features are normal, the eGFR and creatinine in serum serve as the primary indicators in this cluster for early signs of impairment, as they fall within the threshold of normal kidney function. These values suggest a risk of early-stage CKD in asymptomatic patients, and they are crucial to regularly monitor them for these individuals.

Machine learning for automatic cluster classification

We fed our 1545 records to several ML algorithms along with the three clusters. Our training set contained 80% of the data, whereas the testing set contained 20% with 10-fold cross validation. Table 5 compares the performance of these algorithms, including random forest (RF), support vector machine (SVM), logistic regression (LR), neural network (NN), naive Bayes, and gradient boosting, in terms of the AUC, accuracy, F1 score, precision, recall, and Matthew’s correlation coefficient (MCC).

Table 5 Comparison of several ML models.

Figure 5a shows the ROC and (b) shows lift curves of the gradient boosting model in classifying the three clusters. The ROC curves for all three clusters illustrate that the model has perfect performance in all cases. Furthermore, the rapid increase in lift at low P rates suggests that the model is effective at identifying a large proportion of positive cases in the top segment.

The confusion matrix for the testing set shows that 127 were classified in cluster 1, 150 in cluster 2, and 32 in cluster 3; none of the clusters were incorrectly classified. This demonstrates that the dataset’s clustering method was optimal.

We found that the gradient boosting model performed the best. Therefore, we selected it to classify external validation data consisting of 400 records lacking target labels.

After applying the gradient boosting model for prediction, we obtained 151 records in cluster C1, 202 records in cluster C2, and 47 records in cluster C3. With 400 total records, a chi-square statistic of 800, 4 degrees of freedom, and a p value of 0, we have strong evidence to reject the null hypothesis and conclude that there are significant differences among the groups in the validation dataset.

Using multiple feature importance metrics in Fig. 5, the eGFR feature is the most vital feature for kidney function analysis, with the highest importance across all metrics (information gain, gain ratio, and chi-square). This gives evidence to the fact that eGFR is a significant feature for diagnosing CKD. Other features, including albumin in serum, sodium (Na) in serum, and gender, are critical for evaluating kidney health. Cluster C2 indicates these individuals who may have slight problems with their kidneys but do not show symptoms of kidney disease.

The feature importance rankings confirmed the importance of other indicators, like blood creatinine. They also showed how important other features were, such as calcium, total protein, and electrolyte levels. These results show how vital it is to use non-traditional markers (like calcium and albumin) in regular screenings to find CKD that doesn’t have any symptoms. This study shows that it is critical to use regular laboratory data along with ML to detect patients who don’t have symptoms.

BMI ranked 14th out of 18 features, with consistently low scores across metrics such as information gain (0.010), gain ratio (0.006), chi-square (2.178), and ReliefF (0.003). These results suggest that BMI has minimal predictive impact for CKD results in our dataset. However, BMI remains an important clinical indicator of an individual’s health, and its inclusion in clinical models may enhance interpretability for practitioners. The proposed ML model didn’t use BMI as an important feature, but its Spearman correlation with eGFR (r = − 0.404) suggests a possible indirect link with kidney function. This study doesn’t fully look at how BMI might affect the progression of CKD because it doesn’t look at the inflammation that is linked to obesity, high blood pressure, or diabetes.

We could not verify that the training and validation datasets are statistically identical due to the presence of missing values; this was an intentional choice to test the model’s robustness and applicability in situations where incomplete data is a challenge. We collected these datasets with consistent inclusion and exclusion criteria, reflecting the target population. However, the validation dataset includes missing values to mimic real-world scenarios where incomplete data is common. This method allows us to assess the model’s performance in reality, ensuring that it can manage problems like missing or noisy data. The inclusion of missing values adds a controlled difference, focusing on evaluating the model’s robustness and ability to generalize to real-world settings rather than the datasets’ strict statistical similarities. Collecting data from a single lab center ensures that measurement procedures are always the same, removing any differences that could be caused by things like device calibration or assay methods. This increases the reliability of the data. The recursive embedding and clustering technique effectively integrates hierarchical relationships, decreases dimensionality, and maintains significant features. This approach is especially useful for identifying small patterns, such as those present in early-stage asymptomatic CKD, which are usually challenging to detect.

Despite the model’s performance, we must acknowledge some limitations. Firstly, the dataset’s 2,000 records originated from a single source, potentially limiting its generalizability to more diverse or larger populations. Therefore, the lack of external validation is still a limitation, and future research should focus on testing the model on larger and more varied datasets to make sure it can be used in a variety of clinical settings. Finding an appropriate strategy for dealing with the high computing costs of embedding and clustering large data sets is important as well.

Conclusion

CKD encompasses a series of conditions and a major health concern that can ultimately result in kidney failure. Early signs of poor renal function may not be detected through routine tests. This study applied a recursive embedding and clustering technique to 1600 real records to reveal clusters that contain features with midrange and normal values. The combination of these features can assist clinicians in focusing on individuals yielding these values in their routine tests, serving as early signs to prevent the more serious consequences of later CKD stages. We measured the correlations between features and applied ML along with clustering to identify asymptomatic cases. Our results were validated with an additional 400 records with unlabeled data. Our study results are crucial for improving disease management and preventing disease progression. The proposed methods could also be generalized to detect other diseases in clinical practice. In the future, we will attempt to combine our technique with deep learning to detect CKD severity from laboratory data as well as medical images. We plan to apply the technique in real time to detect clusters representing midrange and normal values that may consist of a combination of features that can be used to relate CKD to other diseases, such as anemia, diabetes, cardiovascular disease, and hypertension.

Fig. 1

Flowchart for the proposed method.

Fig. 2

Evaluation of imputation methods for the BMI feature.

Fig. 3

Visualization of the data in the three resulting clusters used for training and testing (a), visualization of the validation data as three distinct clusters (b), mean values for features across clusters (c).

Fig. 4

Sieve diagrams for understanding feature characteristics.

Fig. 5

ROC curves for the C1, C2, and C3 clusters (a), lift curves for the C1, C2, and C3 clusters (b), features importance metrics (c).