There’s a famous story where Gauss was asked to sum the integers from 1 to 100 in elementary school. He noticed a pattern and came up with a formula to sum 1 to N in constant time (source: https://www.nctm.org/Publications/TCM-blog/Blog/The-Story-of-Gauss). The formula is:
Every now and then you need to sum integers from 1 to N in a math or programming problem and this formula comes up. Today I hit it while working with fully connected graphs. With 2 nodes there is only 1 connection in the graph. With 3 nodes there are 3 connections. With 4 nodes there are 6 connections and so on.
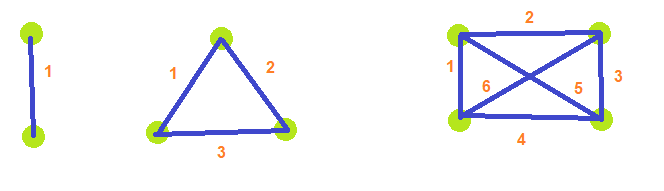
If you notice, the number of connections in a graph with M nodes is the sum of all integers from 1 to M-1. So, with M nodes, you plug M-1 into Gauss’ formula, and it tells you the number of connections there are. You now know how much memory your need to allocate, the size of your for loops etc.
| Nodes | Connections | Sum |
| 2 | 1 | 1 |
| 3 | 3 | 1+2 |
| 4 | 6 | 1+2+3 |
| 5 | 10 | 1+2+3+4 |
| 6 | 15 | 1+2+3+4+5 |
| 7 | 21 | 1+2+3+4+5+6 |
| 8 | 28 | 1+2+3+4+5+6+7 |
That is nifty, but I also wanted to enumerate all the connections in a for loop and get the nodes involved in each connection. That is a little more challenging. Here are all 6 connections in a 4 node graph.
| 0-1 | 0-2 | 0-3 |
| 1-2 | 1-3 | |
| 2-3 |
For counting purposes, let’s start at 0-1 as index 0, then 0-2 as index 1, 0-3 as index 2, 1-2 as index 3 and so on until 2-3 which is index 5.
So let’s say you are at index 4 (which is 1-3). Can you come up with an algorithm to turn that connection index into the pair of nodes that are involved in that connection?
One way to do this is to see that the first group has 3 items in it, so if the index is less than 3, you know it’s in the first group. Else you subtract 3 and then see if it’s less than 2, which is the size of the second group. You repeat this until you know what group it is. in. The group determines the first node in the connection. From there, you can add the remainder of the index value, plus 1, to get the second node in the connection.
That algorithm works, but it’s iterative and the more nodes you have, the slower the algorithm gets. That is no good.
Luckily there is a better way!
Firstly, you can reverse the problem by subtracting your index (4) from the number of connections minus 1.
6 – 1 – 4 = 1.
Doing so, the connections reverse order and become the below, and you can see that 1-3 is at index 1.
| 2-3 | ||
| 1-3 | 1-2 | |
| 0-3 | 0-2 | 0-1 |
Now the problem becomes: “For what N do i have to sum integers from 1 to N to get to my index?”
Knowing that lets you calculate which group an index is part of, and thus the first node in the connection. The relative position of the index within in the group lets you calculate the second node in the connection. This algorithm is similar to the one described before, but there is no loop. It will run the same speed whether you have 10 nodes or 10,000 nodes!
However, to be able to answer that question we need to be able to invert Gauss’s function. We want to plug in a y and get an x out.
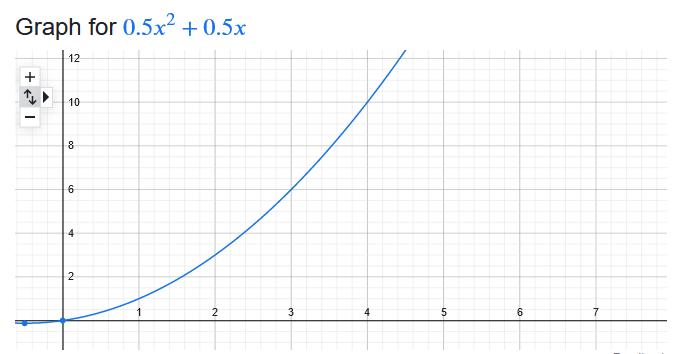
We need to swap y and x in that formula and solve for y again. This 2 minute youtube video is good at explaining how to do that with a quadratic equation: https://www.youtube.com/watch?v=U9dhEoxrA_Y
When done, you should end up with this equation:
The actual result will have a + and – in front of the square root, but we know we are only interested in positive solutions, so we are ignoring the negative solutions.
When you plug values into this formula, you will get non integers sometimes. You just floor the result to get the value you are interested in. This is really answering “what N gets closest to my index without going over?”. The table below shows the equation in action.
| Value | N (in sum 1 to N to get to this value without going over) | floor(N) |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 1.6 | 1 |
| 3 | 2 | 2 |
| 5 | 2.7 | 2 |
| 6 | 3 | 3 |
| 8 | 3.5 | 3 |
| 10 | 4 | 4 |
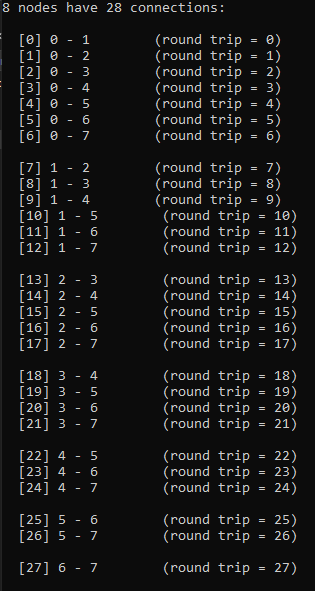
Now that we have inverted Gauss’ formula, we are ready to solve the challenge of turning a connection index into the pair of nodes that are involved in that connection. Below is a small C++ program and the output, to show it working.
As a bonus, it also shows how to convert from a pair of nodes back to the connection index.
#include <stdio.h>
#include <cmath>
// The number of nodes in the graph
static const int c_numNodes = 8;
// Returns the sum of 1 to N
inline int GaussSum(int N)
{
return N * (N + 1) / 2;
}
// Returns the floor of the possibly fractional N that is needed to reach this sum
inline int InverseGaussSum(int sum)
{
return (int)std::floor(std::sqrt(2.0f * float(sum) + 0.25) - 0.5f);
}
// Returns the index of the connection between nodeA and nodeB.
// Connection indices are in lexographic order.
int NodesToConnectionIndex(int nodeA, int nodeB, int numConnections, int numGroups)
{
// make sure nodeA < nodeB
if (nodeA > nodeB)
{
int temp = nodeA;
nodeA = nodeB;
nodeB = temp;
}
// Find out where the group for connections starting with nodeA begin
int groupIndex = nodeA;
int reversedGroupIndex = numGroups - groupIndex - 1;
int reversedGroupStartIndex = GaussSum(reversedGroupIndex + 1);
int groupStartIndex = numConnections - reversedGroupStartIndex;
// add the offset acocunting for node B to get the final index
return groupStartIndex + (nodeB - nodeA - 1);
}
// Turn a connection index into two node indices
inline void ConnectionIndexToNodes(int connectionIndex, int numConnections, int numGroups, int& nodeA, int& nodeB)
{
// Reverse the connection index so we can use InverseGaussSum() to find the group index.
// That group index is reversed, so unreverse it to get the first node in the connection.
int reversedConnectionIndex = numConnections - connectionIndex - 1;
int reversedGroupIndex = InverseGaussSum(reversedConnectionIndex);
nodeA = numGroups - reversedGroupIndex - 1;
// If we weren't reversed, the offset from the beginning of the current group would be added to nodeA+1 to get nodeB.
// Since we are reversed, we instead need to add to nodeA how far we are from the beginning of the next group.
int reversedNextGroupStartIndex = GaussSum(reversedGroupIndex + 1);
int distanceToNextGroup = reversedNextGroupStartIndex - reversedConnectionIndex;
nodeB = nodeA + distanceToNextGroup;
}
int main(int argc, char** argv)
{
// Calculate how many connections there are for this graph
static const int c_numConnections = GaussSum(c_numNodes - 1);
static const int c_numGroups = c_numNodes - 1;
// Show stats
printf("%i nodes have %i connections:\n", c_numNodes, c_numConnections);
// show the nodes involved in each connection in the graph
int lastNodeA = -1;
for (int connectionIndex = 0; connectionIndex < c_numConnections; ++connectionIndex)
{
int nodeA, nodeB;
ConnectionIndexToNodes(connectionIndex, c_numConnections, c_numGroups, nodeA, nodeB);
if (nodeA != lastNodeA)
{
lastNodeA = nodeA;
printf("\n");
}
int roundTripIndex = NodesToConnectionIndex(nodeA, nodeB, c_numConnections, c_numGroups);
printf(" [%i] %i - %i (round trip = %i)\n", connectionIndex, nodeA, nodeB, roundTripIndex);
}
return 0;
}
Alternate Option #1
Daniel Ricao Canelhas says…
If you are looking for the node indices that correspond to a particular edge index in a fully connected graph, you can use the triangular root of the edge index. The maths work out essentially the same as in your post, but the ordering seems to be a bit different.
suppose you have a triangular matrix G representing your graph:

where each entry in the matrix is the index of an edge and the row and columns are the nodes joined by that edge (the diagonal is missing, since no node is connected to itself).
so given an arbitrary edge number, how do you find the two nodes (row, column, respectively) that are joined by it?
take edge index e and obtain the row as
row = floor( (sqrt(8*e+1) - 1)/2) + 1
then get the column as
s = (row * ( row - 1))/2col = e - s

Not that you need to construct that matrix. As you observe, you simply need to loop through the edges which, for a fully connected graph you know to be, for N nodes:N*(N-1)/2
The above gives you the zero-based index directly, which is nice for accessing elements in arrays. It is also useful since you can take e as a global thread index for e.g. GPGPU compute kernels when doing work in parallel.
it was an implementation detail in a paper (http://oru.diva-portal.org/smash/get/diva2:1044256/FULLTEXT01) i wrote when i was a grad student. Perhaps you’re using this in a similar application (creating a fully connected graph and pruning it by processing all the edges in parallel)
Alternate Option #2
@knavely says (https://twitter.com/knavely/status/1693996686312653299)

With the link here: https://github.com/knavely/sherali_adams/blob/master/sherali_adams/sherali_adams.py
Closing
Hacker news discussion of this post: https://news.ycombinator.com/item?id=37219121

I found the use of floating point dubious and eliminated it, for me the float code here is intermittently wrong starting at GaussSum(5793). https://news.ycombinator.com/item?id=37220519
LikeLike
Nice improvement!
LikeLike
Pingback: Permutation Iteration and Random Access « The blog at the bottom of the sea