Momentum prediction models of tennis match based on CatBoost regression and random forest algorithms

Abstract

As we all know, momentum plays a crucial role in ball game. Based on the 2023 Wimbledon final data, this paper investigated momentum in tennis. Firstly, we initially trained a decision tree regression model on reprocessed data for prediction, and established the CBRF model based on CatBoost regression and random forest regression models to obtain prediction data. Secondly, significant non-zero autocorrelation coefficients were found, confirming the correlation between momentum and success. Thirdly, Based on these key factors, we proposed winning strategies for the players, conducted predictive analyses for six specific time intervals of the game. At last, by implementing these models to women’s matches, championships, matches on different surfaces, the results demonstrated that the models have effective generalization ability.

Introduction

In the 2023 Wimbledon men’s final, 20-year-old Spanish rising star Carlos Alcaraz triumphed over 36-year-old tennis legend Novak Djokovic. This thrilling tennis showdown ended Djokovic’s Grand Slam record at Wimbledon since 2013 and marked a significant historical shift for Wimbledon. After numerous intense twists and turns, Alcaraz ultimately emerged victorious by a set margin. The match was dramatically fluctuating, with the lead constantly changing between the two, culminating in Alcaraz’s victory, showcasing his resilience and ability to transform the tide in adversity. Many refer to these situations as a shift in “momentum”, believing that changes in momentum can sometimes influence the direction and even the outcome of a match.

There has been a proliferation of research on momentum in sport and competition, with momentum being categorised as strategic and psychological momentum. In 2017, Page et al. designed an experimental approach to test the win/loss effect, exemplifying the role of momentum in ball games¹, and in 2018 and 2019, an experiment was proposed to validate the lesser role of psychological momentum using data from football matches^2,3. In 2019, a reflection of men’s strategic momentum was discovered in professional tennis matches an evidence that examined Grand Slam women’s singles matches to find the value of applying methods to evaluate players⁴. Fitzpatrick A. et al. tested a new approach to identifying important performance characteristics requiring a large amount of data from elite tennis matches, demonstrating consistency with standard statistical methods⁵. In⁶, the authors stressed the importance of tennis training skills, strategies, etc. In⁷, the authors evaluated the generality of the results by applying the momentum metaphor to women’s college basketball. Zhu X. analysised the technical and tactical characteristics of Novak Djokovics Serve in different types of tennis courts⁹. Tao Q. studied the winning and losing factors of women’s singles tennis tournaments in different tennis courts¹⁰. In¹¹, they discussed important performance characteristics in elite clay and grass court tennis match-play. Wang Z. constructed a mathematical model of momentum heuristic to analyse and predict realistic problems¹². Although the concept of “momentum” has been widely considered in sports, how it can be quantitatively analyzed and its effect on match results remains a puzzle.

In recent years, the rise of artificial intelligence algorithmic methods such as multivariate statistical analysis¹⁴, machine learning^15,16, and decision trees¹⁷, BP network¹⁸ has led to more and more extensive applications in prediction.

Inspired by the above literature, This paper analyses the momentum of tennis using CatBoost regression and Random Forest algorithm, which will help you to catch the trend of the competition and ultimately achieve the desired results. The main work is illustrated in Fig. 1.

Figure 1

Our work.

The main innovations and contributions are as follows:

• (1) The CBRF prediction model based on CatBoost regression and random forest regression models was established, and During the model-building process, we reduced the main variables affecting the game’s momentum to three dimensions using Principal Component Analysis to simplify the model’s complexity, that was to capture the momentum shifts in tennis matches and determine which player performs better at a given time and to what extent⁷.

• (2) Significant non-zero autocorrelation coefficients were found, confirming the correlation between momentum and success in the game. Using the model, these changes in momentum during a match are correlated with the scoring.

• (3) Through feature importance parameters within the model and Spearman correlation analysis, we developed a predictive model using match data to identify the factors that most significantly influence scoring, and proposed winning strategies taken into account these factors.

• (4) We introduced the total distance covered by the players as a new variable into the model. We validated the model’s generalization ability by applying it to women’s matches, championships, matches on different surfaces, and in different sports. We compares our model with the DPI model²¹ and provides a detailed description of the construction methods and performance metrics of the DPI model. A visual comparison is used to show the differences in prediction accuracy between the CBRF model and the DPI model, further emphasizing the advantages of the CBRF model.

In section “Assumptions and notations”, we introduced assumptions and notations, and listed common variables in the formulas along with their meanings. In section “Data preprocessing and exploratory analysis”, we conducted preprocessing of data before modeling. In section “Use models to capture momentum changes”, we designed CBRF prediction model to capture momentum changes. In section “Competition impacts success”, we researched autocorrelation analysis (ACF/PACF) on the predicted values, and obtained the forecast data of momentum. In section “Using metrics to assess the competition process”, match data was analyzed by using the developed model to investigate the variables that have the most significant impact on the momentum shift in matches. In section “Exploration of model generalization”, we applied the data of Wimbledon Tennis Championships, women’s tennis matches and different Playing Surfaces to justify the performance of our model. At last, we also made sensitivity analysis, model comparison and model evaluation in sections “Sensitivity analysis”, “Model comparison” and “Model evaluation”.

Assumptions and notations

Assumptions

To simplify our model, we make several general assumptions listed below along with their corresponding rationales:

• (1) It is assumed that players will not be affected by unexpected injuries during the match.

  In regular matches, players often suffer accidental injuries during intense confrontations. They tend not to leave the game, but this may negatively affect their condition. However, in our assumption, they are considered not to be affected.

• (2) It is assumed that both competitors will be unaffected by changes in weather conditions. Weather changes during matches are unpredictable, and different players have varying abilities to adapt to sudden weather changes. Therefore, we assume they will be unaffected by the weather.

• (3) It is assumed that players’ decisions and actions are aimed at maximizing their scoring probability. There are instances in matches where players may lose points intentionally for tactical and strategic implementations. We assume that players are subjectively acting to score points.

• (4) It is assumed that the provided tennis match dataset can adequately reflect the general rules of the entire match.

Since we only have the dataset of men’s singles matches from the second round of the 2023 Wimbledon Tennis Open, the data may do not necessarily reflect all aspects of the matches. Thus, we assume this dataset can capture key factors influencing the match progress to a certain extent.

Symbol representation

In Table 1, we have listed the key symbols used in the paper.

Table 1 Symbol representation.

Data preprocessing and exploratory analysis

Data collection and preprocessing

To analyze and establish a reasonable mathematical model for predicting the momentum shifts in tennis matches, analyzing the relevant data provided is essential. The original data-set comes from the men’s singles matches data-set after the second round of the 2023 Wimbledon Tennis Open²⁰.

For handling missing values in the original dataset, we used Python to process these missing values. By dealing with null and NA values, we identified 752 missing values for the speed-mph variable, 54 missing values for the serve-width variable, 54 missing values for the serve-depth variable, and 1309 missing values for the return-depth variable. Given the importance of these variable features, we opted to fill in missing values with the median of the respective variables to ensure data consistency and completeness, as shown in Table 2 below:

Table 2 Missing data value.

For the detection of outliers, we employed the 3-sigma rule for outlier identification and did not find any outliers. To reduce the complexity of handling data in machine learning, we transformed the Return-depth variable, setting D (Deep) as 0 and ND (Not Deep) as 1. For the Serve-depth variable, NCTL (Not Close To Line) was set as 1 and CTL (Close To Line) as 0. The Serve-width variable was coded as follows: B (Body) as 1, BC (Body/Center) as 2, BW (BodyWide) as 3, C (Center) as 4, W (Wide) as 5. For the Winner-shot-type variable, F (Forehand) was set as 1 and B (Backhand) as 2. Regarding the elapsed-time variable with “h:mm:ss” time data, to facilitate model understanding, we converted it into “ss” (total seconds) format. In p1-score and p2-score, AD represents a scoring state exceeding the opponent’s, thus we transformed it into a value above 40; here, we set $AD = 50$¹⁰. This is illustrated in Table 3.

Table 3 Data replacement.

To enhance the model’s performance and reduce computation time, we applied PCA¹⁴ (Principal Component Analysis) for data dimensionality reduction, reducing the main variables affecting point-victor to three dimensions.

Data description and exploratory analysis

To aid in modeling, we visualized the data, which helps us uncover the relationships between different variables. We used Python visualisations for the simulations, Figure 2 shows the frequency distribution of the set-no and game-no variables in histograms, Figure 3 displays the distribution of the three principal components after dimensionality reduction.

Figure 2

The frequency of parameter in the competition.

Figure 3

Principal component distribution.

From Fig. 2, it can be observed that the frequency of “2” in the set-no variable is the highest, and the frequency of “6” in the game-no variable is the highest. From Fig. 3, it is evident that PCA1 and PCA2 account for the major trend of variation in the data, while PCA3 explains a lesser extent of the variation trend.

Use models to capture momentum changes

In this section, we are tasked with developing a model capable of capturing momentum to describe the probability of scoring in a match. For this purpose, we have chosen a stacking model strategy and established the CBRF (Composite Bayesian Regression Framework) prediction model to describe the match process. The flowchart of this model is illustrated in Fig. 4.

Figure 4

Modeling.

Based on decision tree CatBoost regression prediction model

Decision tree regression model

The process of generating a decision tree involves continuously grouping the training sample set. The branches of the decision tree grow gradually as the data is segmented further. The core technique in the growth of a decision tree is the test attribute selection issue¹². We use the data after dimensionality reduction as the independent variable and point-victor as the dependent variable to conduct machine learning with the decision tree regression prediction model, obtaining the predicted model results.

When utilizing machine learning algorithms for predictions, it’s common practice to assess the accuracy of these predictions using several statistical metrics. These metrics include Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and the Coefficient of Determination $R^{2}$ The formulas for calculating these metrics are as follows:

$$\begin{aligned} MSE= & {} \frac{1}{N}{\textstyle \sum _{i=1}^{N}}(y_{i}-{\hat{y}}_{i})^{2},\\ RMSE= & {} \sqrt{\frac{1}{N}{\textstyle \sum _{i=1}^{N}}(y_{i}-{\hat{y}} _{i} )^{2}},\\ MAE= & {} {\frac{1}{N}{\textstyle \sum _{i=1}^{N}}\left| y_{i}-{\hat{y}} _{i}\right| },\\ MAPE= & {} {\frac{100\%}{N}{\textstyle \sum _{i=1}^{N}}\left| \frac{y_{i}-y_{i}^{'}}{y_{i} }\right| },\\ R^{2}= & {} 1-\frac{{\textstyle \sum _{i=1}^{N}}(y_{i}-{\hat{y}}_{i})^{2}}{{\textstyle \sum _{i=1}^{N}}(y_{i}-{\bar{y}}_{i})^{2}}. \end{aligned}$$

In the context provided, $y_{i}$ represents the actual value of the $i{\text {th}}$ sample, ${\hat{y}} _{i}$ is the predicted value of the $i{\text {th}}$ sample, N is the total number of samples,${\bar{y}}$ is the average of all actual values.

Using the formulas provided above, the results can be calculated and presented as shown in Table 4:

Table 4 Decision tree evaluation results.

Upon analyzing the evaluation results from Table 1, it was found that the value was too small. Therefore, we decided to optimize the decision tree regression prediction model and adopt the CatBoost regression prediction model for re-prediction.

CatBoost regression prediction model based on decision tree regression model

CatBoost is a framework that relies on symmetric decision trees as base learners, characterized by fewer parameters and support for multivariate analysis. Its primary advantage lies in efficiently and reasonably addressing prediction bias, thus minimizing overfitting and enhancing the model’s accuracy and generalizability¹³. The expression for this model is:

$$\begin{aligned} x_{i,k} =\frac{ \sum _{j=1}^{p-1} [x_{\sigma _{j,k} }=x_{\sigma _{p,k} } ]\cdot Y_{j}+ a\cdot p }{\sum _{j=1}^{p-1} [x_{\sigma _{j,k} }=x_{\sigma _{p,k} } ]+a}. \end{aligned}$$

In the formula, $\sigma _{j}$ represents the model’s output for the $j{\text {th}}$ data point; $x_{i,k}$ denotes the discrete feature in the $k{\text {th}}$ column of the $i{\text {th}}$ row in the training dataset; a is a prior weight; and p represents the prior distribution term. The predicted model results are evaluated, with the evaluation results presented in Table 5, and the formulas for calculating evaluation result parameters are provided in section “Decision tree regression model”.

Table 5 CatBoost regression prediction model evaluation results.

Although this model fits the data significantly better than the random forest model, its predictive performance is still not ideal. While the model performs well on training data, its performance degrades significantly on test data, exhibiting increased prediction errors and reduced accuracy. Furthermore, the coefficient of determination is very high on the training set but decreases markedly on the test set, indicating a problem of overfitting.

Building the CBRF prediction model based on CatBoost regression model and random forest regression model

To make the model more accurate, considering that in tennis matches, the serving side often has a higher probability of scoring²², we incorporate the serving side’s weight $S_{i}$ as an additional variable into the CatBoost regression model. This way, the model’s prediction function depends on both the original data $S_{i}$ and the serving side’s weight $S_{i}$.

$$\begin{aligned} {\hat{y}}_{i}^{(CB)}=f_{CB}(X_{i},S_{i}). \end{aligned}$$

In this context, ${\hat{y}}_{i}^{(CB )}$ represents the predicted probability of winning, while $f_{CB}$ is the prediction function constructed using the CatBoost regression model.

Besides this, random Forest is a supervised machine learning method constructed through an ensemble of decision trees as base learners. It introduces randomness into the decision tree training process, endowing it with excellent anti-overfitting and noise resistance capabilities¹⁶.

To make machine learning predictions more accurate, we stack the CatBoost regression model on top of the Random Forest regression model to construct the CBRF prediction model. In this model, we use the prediction results from the CatBoost regression model as input data to build the Random Forest regression model:

$$\begin{aligned} {\hat{y}} _{i}^{(CBRF)} =f_{CBRF} \left( {\hat{y}} _{i}^{(CB )},S_{i},X_{i}^{'} \right) . \end{aligned}$$

In this expression, ${\hat{y}} _{i}^{(CBRF )}$ represents the predicted value from the CBRF prediction model, and $f_{CBRF}$ is the prediction function of the CBRF prediction model, which incorporates variable $S_{i}$.

Additionally, to enhance the accuracy of the model training, we employ three-fold cross-validation to assess the model’s stability during the training process. The ratio of the training set to the dataset in the total data is 4:1.

After training, we obtain the predicted results for ‘point-victor‘. Comparing these predicted results with the original values of ‘point-victor‘, and considering the large volume of original data, we select the predicted results of one match for visualization, resulting in Fig. 5 as shown:

Figure 5

Scorer prediction.

From the above figure, it is evident that the predicted values are very close to the actual values.

Predictive evaluation analysis

The predicted model results are evaluated, with the evaluation results presented in Table 6, and the formulas for calculating evaluation result parameters are provided in section “Decision tree regression model”.

Table 6 Evaluation of CBRF model predictions.

The data from the table indicate that the values of MSE, RMSE, MAE, and MAPE are all low, and $R^{2}$ is close to 1. Therefore, it can be concluded that the CBRF prediction model exhibits very good predictive performance on the dataset of men’s singles matches from the second round of the 2023 Wimbledon Tennis Open. This demonstrates that the model can accurately predict the direction of matches based on the momentum of the athletes, proving the effectiveness of the CBRF prediction model in this task.

Figure 6

Example.

We use Python visualisers for simulation, and from the Fig. 6, it can be analyzed that the prediction results for both the training and test sets are similar. This indicates that the CBRF prediction model has good generalization ability and does not exhibit overfitting or underfitting phenomena.

Score probability visualization

Through the establishment of the CBRF prediction model, we have been able to determine who is more likely to be the scorer as a result of momentum shifts. However, we are yet unable to visually represent which player performs better at a specific moment in the match and to what extent. Therefore, we propose constructing the following model to describe this:

$$\begin{aligned} \theta _{1}= & {} \left( 2-{\hat{y}}^{(CBRF)} \right) \times 100\%,\\ \theta _{2}= & {} \left( 1-{\hat{y}}^{(CBRF)} \right) \times 100\%, \end{aligned}$$

where $\theta _{1}$ represents the probability of Player 1 winning, $\theta _{2}$ represents the probability of Player 2 winning.

We visualize the probabilities $\theta _{1}$ and $\theta _{2}$ to express this concept, as shown in Fig. 7 below, we used Python to visualise and analyse the data.

Figure 7

Visualization of scoring probability.

From the chart, you can observe the probability of each player scoring at a specific time interval. For instance, in the case of Player 1 during the match at 1301 s, the probability of winning is 3.72%, while at 4806 s, the probability of winning jumps to 95.74%.

Competition impacts success

A tennis coach is skeptical about the role of momentum in matches, believing that fluctuations and a player’s success are random. However, through analysis, we contend that fluctuations and a player’s success in matches are correlated.

Autocorrelation (ACF)¹⁵ refers to the degree of correlation between a sequence and its lagged version, while the Partial Autocorrelation Function (PACF) measures the conditional correlation between two sequences, given other sequence terms. By conducting autocorrelation analysis (ACF/PACF) on the predicted values, we obtain the predicted data, one can see Fig. 8.

Figure 8

ACF/PACF.

From Fig. 8, it is observed that there are autocorrelation coefficients significantly outside the confidence interval (i.e., significantly non-zero), indicating that the predicted values are not purely random and exhibit some form of autocorrelation.

To identify the factors that most significantly influence scoring, we adjust the dependent variable in the CBRF prediction model to the ‘p1-points-won‘ variable, with independent variables set to match time, the number of sets won by player 1, and other significant variables, and retrain the model to obtain predicted values for ‘p1-points-won‘. We use Python visualisers for simulation, then visualize and compare the predicted values of ‘p1-points-won‘ with the actual values, resulting in Fig. 9:

Figure 9

Visualization of score trend.

From the above graph, it can be observed that the trend of predicted values is closely aligned with the trend of actual values. This indicates that the impact of momentum in the match is evident. Therefore, fluctuations in the match and a player’s success are correlated and not random¹².

Using metrics to assess the competition process

Key factors affecting scores

In this section, we will analyze the match data using the developed model to investigate the variables that have the most significant impact on the momentum shift in matches. During the above training of CBRF, we observed that different variables had varying levels of importance in predicting the outcome. Analysed by spasspro software, we utilized the feature importance parameter inherent to the Random Forest regression model to determine the feature importance of each variable. The results are displayed in Fig. 10:

Figure 10

Importance of variable characteristics.

Figure 11

Spearman correlation analysis.

Analysed by origin software, we get spearman correlation analysis in Fig. 11, it can be observed that variables such as ‘p1-unf-err‘ and ‘p2-winner‘ have a significant impact on the model’s predictive results. Therefore, we conducted Spearman correlation analysis on these important variables. The Spearman correlation coefficient is a non-parametric measure that describes the degree of the relationship between two variables using a monotonic function. Based on the analysis, a heatmap was generated.

Analyzing the data in Fig. 11, it can be observed that ‘p1-unf-err‘, ‘p2-winner‘, ‘server‘, and ‘point-victor‘ are correlated. Therefore, the non-forced errors committed by Player 1, the unreturnable winners hit by Player 2, and the server’s performance have a significant impact on the points won in a particular game.

Strategies for achieving high scores

Based on our analysis of the above problem, it is evident that Player 1’s non-forced errors, Player 2’s unreturnable winners, and the server’s performance have a significant impact on points won in a game. Therefore, we have formulated the following strategies to help players achieve higher scores in new matches, one can see Fig. 12:

• Ensure Adequate Sleep and Reduce Pre-match Pressure: This can help players reduce non-forced errors caused by lapses in concentration or incorrect judgments during matches, improving overall stability.

• Targeted Analysis of Opponents: Analyzing opponents can help players better respond to their opponents’ strategies, reducing non-forced errors in specific situations and countering unreturnable winners effectively.

• Improve Serving Quality and Variety: Enhancing serving skills allows players to leverage their serving advantage to control the pace of the game.

• Strengthen Return of Serve Training: Focusing on return of serve training can help players improve their ability to break their opponents’ serves and increase their chances of winning points in non-serving games.

Figure 12

Winning strategy.

Exploration of model generalization

Analysis of Wimbledon tennis championships

In order to delve deeper into the performance of our model in predicting individual tennis matches, we have selected the following six matches from the 2023 Wimbledon Tennis Championships for analysis.

2023-wimbledon-1301	2023-wimbledon-1309	2023-wimbledon-1401
2023-wimbledon-1408	2023-wimbledon-1502	2023-wimbledon-1701

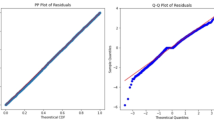
These matches were individually input into our pre-trained CBRF model for predictive analysis, thus yielding the corresponding prediction outcomes. Residuals, which represent the differences between actual values and predicted values in mathematical statistics, encapsulate critical information regarding the fundamental assumptions of the model. We use Python visualisation for simulation, and generated residual plots for these six match prediction data, as shown in Fig. 13.

Figure 13

Residual prediction data.

Through the observation of the residual plot, we have noticed that the residuals are predominantly distributed around the horizontal line, indicating that there is no systematic bias in the predictions. However, it is evident from the plot that the residuals follow a radial pattern with respect to the predicted values, suggesting the presence of outliers or anomalies. As a result, we have conducted an evaluation of the prediction outcomes, as outlined in Table 7:

Table 7 Evaluation of the results of the forecasting set.

From the evaluation of the prediction outcomes, we can observe an increase in the evaluation metric values, indicating that the model’s predictive performance is suboptimal for specific matches. It is possible that other feature variables are influencing these matches. Based on our data analysis and observations, we believe that the physical fitness of the players has an impact on the prediction results. Consequently, we have incorporated the total distance covered by the players in this match as a new feature variable in our model training. The formula for calculating the total distance covered is as follows:

$$\begin{aligned} RD=\sum _{i=1}^{P_{n} } d_{i}, \end{aligned}$$

where, RD represents the total distance covered, $P_{n}$ represents the number of points scored in the match (Point-no), $d_{i}$ represents the distance run for each point scored (P1-distance-run).

We perform simulation analysis by spasspro, after incorporating variable RD into the model and retraining it, we have recalculated the feature importance scores for each variable, as shown in Fig. 14.

Figure 14

Importance of new variable features.

Analysis reveals that RD has an importance factor of 8.4% in the model, which demonstrates that the physical fitness of players indeed exerts a certain influence on the match momentum and outcomes. Additionally, factors such as season, weather, and other variables may also impact changes in momentum during the matches. These elements are worth thorough consideration by the model to enhance its accuracy and generalization capabilities further.

Analysis of women’s tennis matches and the record of different playing surfaces

Women’s matches and championships

To validate the generalizability of the CBRF prediction model in women’s tennis matches and championships, we selected the 2023 Madrid Final between Iga Swiatek and Aryna Sabalenka as our data source⁸. Using video observation methodology, we recorded each unforced error committed by the players in every scored point, the unreturnable winning shots played by the players, and serving data. These match data were input into the CBRF prediction model for analysis, resulting in prediction outcomes. The scatter plot of the combination of predicted values and actual values is depicted in Fig. 15:

Figure 15

Predictive scatter plot.

The points in this scatter plot are densely clustered around the $y=x$ line, indicating that our pre-trained CBRF prediction model exhibits strong generalizability in women’s matches and championships. We attribute this robust generalizability to the similarity in data types used for training and testing.

Furthermore, the consistency of these results across different matches suggests that the model is not overfitting to specific data points but rather capturing underlying patterns in player performance. This is corroborated by studies such as Wunderlich et al. (2023), which demonstrate that certain performance metrics, such as home advantage, are consistent across genders and levels of competition, reinforcing the notion that predictive models can be generalized beyond their initial training conditions²³.

The record of different playing surfaces

To investigate the applicability of the CBRF prediction model under different playing surface conditions, we selected data from three matches that Novak Djokovic participated in from 2011 to 2015, each representing a different playing surface: hard court, clay court, and grass court⁹. These match data were input into the CBRF prediction model for analysis, resulting in prediction outcomes. We used Python visualisation for the simulation, the scatter plot of the combination of predicted values and actual values is depicted in Fig. 16:

Figure 16

Scatter plots for predicting different sites.

We have observed that the predicted data closely align with the actual data on hard court¹⁰ and clay court, while there is a significant deviation between the predicted data and actual data on grass court. Therefore, the CBRF prediction model demonstrates strong generalizability on hard and clay courts, but it does not perform well in predicting outcomes on grass courts¹¹.

The record of table tennis

We selected data records from a table tennis match in¹⁹ to test the generalizability of the CBRF prediction model we have constructed in different types of sports. While table tennis and tennis share many similarities in their rules, there are still some differences. Therefore, before importing the data, we mapped the obtained table tennis data to tennis data features to enable the model to comprehend table tennis match data. We used Python visualisations for this simulation, after conducting predictive analysis using the CBRF prediction model, we obtained the kernel density estimation plot for predicted data versus actual data, as shown in Fig. 17.

Figure 17

Table tennis Kernel density map.

We have observed that when compared to the actual values, the predicted values exhibit noticeable peaks, and there are differences at some points. Partial successful predictions demonstrate that the CBRF prediction model has a degree of generalizability in table tennis matches. However, the significant differences between the two sports can lead to prediction biases. Therefore, further optimization of the model should be considered to account for the unique factors associated with table tennis.

Sensitivity analysis

To test the sensitivity of the CBRF prediction model, we conducted tests by observing changes in accuracy while altering the weights of input variables. Accuracy was calculated by the proportion of correctly predicted outcomes to the total number of outcomes. We selected three variables: unforced errors, serving speed, and the number of breaks of serve. For each variable, we set three different weight values: high, medium, and low. Therefore, considering the various variables and weights, we obtained a total of 9 accuracy measurements.

Figure 18

Accuracy 3D bar chart.

From Fig. 18, it can be observed that unforced errors and break points won are significant indicators in the model, while serving speed is less crucial. Therefore, adjusting the weights of unforced errors and break points in the model can contribute to an improvement in model accuracy.

Model comparison

In this section, we introduce another model used to capture momentum changes in tennis matches and compare it with the CBRF model. The chosen model is derived from the 2024 MCM paper number 2401445²¹. Its main feature is the introduction of the Dynamic Play Index (DPI) to quantify match flow, and it uses Random Forest classifiers and Hidden Markov Models (HMM) to predict momentum turning points.

Overview of the DPI model

The DPI model proposes the Dynamic Play Index (DPI) to measure match flow. DPI is calculated through a linear combination of Performance (PE), Personal Strength (PS), and Serving Advantage (SA). The specific formula is as follows:

$$\begin{aligned} {D P I=\alpha \times P E+\beta \times P S+\gamma \times S A} \end{aligned}$$

where Performance (PE) is quantified using the Gradient Boosting Trees (GBDT) algorithm based on grid search, predicting a player’s winning probability by analyzing various situational factors in the match; Personal Strength (PS) is summarized through a six-dimensional evaluation index, such as break point conversion rate and average first serve speed; and Serving Advantage (SA) is represented by a binary variable, where the serving player is denoted as 1 and the receiving player as 0. After calculation, the parameters of the formula are determined as:

$$\begin{aligned} {\alpha =0.28, \beta =0.32, \gamma =0.4} \end{aligned}$$

Prediction accuracy comparison

To compare the prediction accuracy of the CBRF model and the DPI model, we analyzed the main performance metrics of both models. The DPI model has a prediction accuracy of 82.4%, while the CBRF model achieves a prediction accuracy of 98.5%. The CBRF model significantly outperforms the DPI model in terms of fit. We created a bar chart to visually present the prediction accuracy of these two models. Figure 19 shows the prediction accuracy of the CBRF model and the DPI model, helping us to better understand the performance differences between the two models.

Figure 19

Model comparison bar chart.

Through this bar chart, we can clearly see that the CBRF model outperforms the DPI model in terms of prediction accuracy. This indicates that although the DPI model has some predictive capability in different match scenarios, the CBRF model excels in overall performance and accuracy. The CBRF model has high prediction accuracy and is suitable for various match scenarios, particularly excelling in predicting momentum turning points, demonstrating its strong generalization ability. Despite its higher computational complexity, the CBRF model’s excellent predictive performance makes it a more reliable choice.

Model evaluation

Advantages

• Comprehensive consideration of multiple variables in matches enhances the model’s interpretability and predictive accuracy, enabling it to effectively capture turning points in matches.

• The adoption of a model strategy that combines CatBoost regression and Random Forest regression reduces the workload in the model preparation stage while maintaining high sensitivity to the data.

• Based on the results of predicting table tennis matches, the model we have built is not only effective in tennis but also exhibits some degree of generalizability to other sports like table tennis.

• During model evaluation, we employed various evaluation metrics to optimize model performance, improving predictive accuracy and generalization capabilities.

• Visualizing player scoring probabilities at different time intervals provides a more intuitive depiction of match dynamics.

Shortcomings

• Variability in applicability on different playing surfaces, with our model showing lower predictive ability on grass courts.

• Challenges in dealing with unique circumstances that can arise during matches, such as weather changes, which to some extent impact the model’s accuracy.

Future work

We plan to enhance the predictive accuracy of the CBRF prediction model for match momentum by collecting more variable data, including players’ psychological states, weather conditions, and other factors. Additionally, we are considering the use of deep learning techniques such as convolutional neural networks (CNNs) to improve the model’s generalization capabilities, allowing it to achieve better predictive results across different playing conditions and various sports.

Conclusions

To investigate the sudden shifts in momentum during the 2023 Wimbledon Men’s Singles final, we proposed a novel model for predicting momentum transitions in the game. Our model can forecast changes in momentum based on real-time match data. The CBRF prediction model we developed combines CatBoost regression and random forest regression, significantly enhancing the accuracy of momentum predictions. Additionally, we visualized the potential scores for players at different time intervals, making the description of the game’s flow more intuitive. Through autocorrelation analysis and predicting the overall score trends of players, we demonstrated that fluctuations in the game are correlated with a player’s success, not random events. Furthermore, we conducted feature importance parameter analysis and Spearman correlation analysis, confirming the significant impact of player 1’s unforced errors, player 2’s unreturnable winners, and the serving side on point acquisition. We also devised strategies for players to achieve higher scores. However, by predicting specific matches, women’s matches, championships, and various surface and sport conditions, we found that the model does not perform well on grass courts and in other sports scenarios. Therefore, future optimization of the model is necessary.