Linear Algebra. SVD and PCA
Want become an expert in Computer Vision & Object Detection?
Subscribe on New Practical Course
SVD
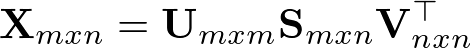
Geometric meaning
The main idea of SVD is that matrix A is basically a linear transformation. And SVD decompose it into 3 factors Rotation(U)*Scaling/Shear(Σ)*Rotation(V).
This gives you interesting posibilities like use it for dimension reduction(that i will show in PCA example), or for point mathching in space
Nice interactive demo: https://www.geogebra.org/m/mrey8VJX
How to compute SVD
- We have matrix A for which we want to compute SVD
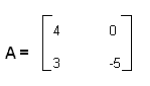
2. We need to compute A.T and gram(A) = A.T * A
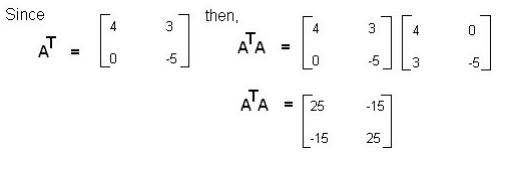
3. From gram(A) we can compute eigenvalues and singular values which will be real, cause gram(A) is NxN size.

Note that singular values should be sorted from biggest to smallest
s1 ≥ s2 ≥ ··· ≥ sn ≥ 0
4. Construct S matrix

5. Now we need find matrix V. For this we need to solve equation gram(A) — cn*I for each eigenvalue, where I — is identity matrix

6. Now we need to find matrix U. If determinant(diag(S)) != 0 we can get U from equation U = A*V*inv(S). In other situation when determinant(diag(S)) != 0 and matrix is Singular (not invertible) we can use formula un = (1/sn) * A * vn, where vn is V[;,n] vector. U = [u1,..,un]

PCA
First of all i want to say that PCA has a brother ICA, and the difference between them can be shown on this image example:

So idea of PCA is a reduction of space, while ICA separating features of that space.
But right now we will talk about PCA, which is simple but still quite usefull things(of course it not the only algo in area of dimension reduction)
How to compute PCA
So we have matrix X. First we will need center it by X/std — mean (by columns)
Then the covariance of X equal
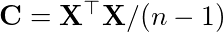
C matrix is symmetric so can be diagonalized
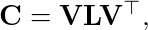
where V — matrix of eigenvectors, L — diagonal matrix of eigenvalue.
The eigenvectors are called principal axes and projection of the data on them principal components (XV)
Now lets perform SVD over X
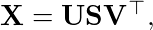
Pasting this into formula of covariance of X will gives us this
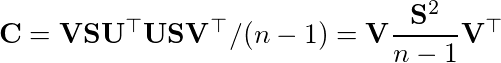
where singular values are related to the eigenvalues of covariance matrix as
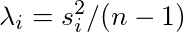
Principal components are given by

So:
- Use SVD on A* and get U, V and S.
- Set new N dimension to which you want to reduce your data. And get first N values from U and S.
Ur= U[:,:n], Sr = S[:n,:n]
3) Reduced(A, N) = Ur * Sr
Of course it’s ony one way of computing PCA, but as i know almost all curent algorithms use SVD(different variations of it) for that, so it most popular.
Code
You can run all this code in Google Colab
Sources
- https://math.berkeley.edu/~hutching/teach/54-2017/svd-notes.pdf
- http://math.mit.edu/classes/18.095/2016IAP/lec2/SVD_Notes.pdf
- https://en.wikipedia.org/wiki/Singular_value_decomposition
Support
Become a Patron and support our community to make more interesting articles & tutorials

